Digital Signal Processing 04 : Sampling Thoery, Nyquist-Shannon Sampling Theorem

Ch04 Sampling(수정중)_221213_221738 (1).pdf

6.45MB

 

 

이론적 배경

1. CTFT

2.  Analog신호를 Digital Processing 하는 방법

(1) Sampling : Time을 주기적으로 디지털화

(2) Quantization : Amplitude를 디지털화

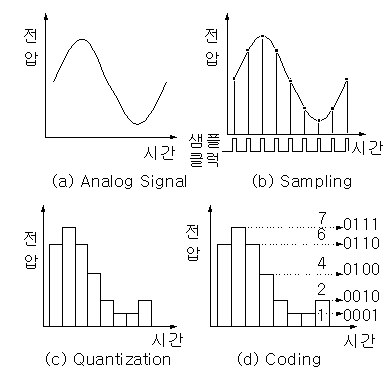
사진 출처 : ADC(Analog-to-Digital Con.. : 네이버블로그 (naver.com), 아날로그 혼성회로

\

사전 용어 정리

sampling이란 아래의 2개 변환 과정과 같다.

x(t) → x_s(T) → x_c(nT) (= x[n])

Sampling 이론

1. 주기적 Sampling, Sampling Frequency(Fs)

(1) Sampling하면 x_continuous(t)가 x[n]으로 바뀜

-둘의 관계는 아래와 같이 정의 가능

- Sampling Frequency : fs(=Fs)로 정의

- Sampling Rate(?) : fs에 2pi를 곱한 각속도 ... 여기서 다루지는 않을 것이다.

- fs가 높을 수록 좀더 analog에 근사한 그래프를 정확하게 얻을 수 있다.

(2) Sampling System의 특징

x(t)와 x[n]은 ADC라는 시스템에서 서로 1:1 대응해야한다.

 

 

 

2. Sampling System을 LTI System의 impulse response(=s(t))으로 정의해보자.

(1) x(t) → x_s(T) 으로 변환

x_c(t)와 s(t)사이에 convolution 표기가 사라졌네? No 원래 곱셈이다!!!

- s(t)는 δ-train의 형태임을 쉽게 알 수있다.

- 그런데 주의사항이 있다. 절대로 x_c(nT)와 x[n]은 같지만, x_s(t)와 x_c(nT)는 서로 다르다 것이다.!!!!

- 그래서 우리는 x_s(t)를 x[n] (=x_c(nt)) 으로 변환해야한다.

(2) Sampling System in time-domain

 

 

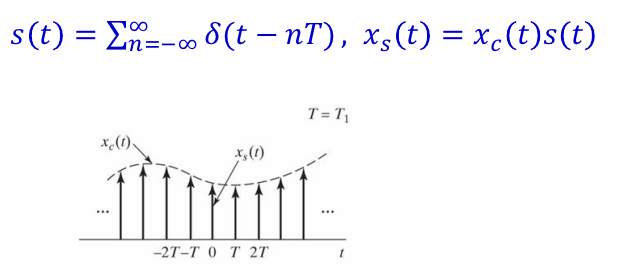
3. Sampling System을 LTI System의 Frequency response(=S(jΩ))으로 정의해보자.

(1) Sampling System in frequency-domain

앞선 2.번의 공식들을 CTFT하면 위와 같고,

이를 Ω-domain에 나타내면 위와 같다.

참고로 (d)를 보면 Baseband signal이 Inter-Simbol Interference(=ISI)(?) 혹은 Aliasing 를 만듦을 알 수 있다. 이러면 원래의 신호로 복조가 불가능한 문제가 있으므로 이를 해결해야한다. 아래의 4.번에서 다루자 (Nyquist-Shannon Sampling Theorem)

(2) 공식 중간 정리

참고로 우리는 위 수식들 처럼, f-domain이 아닌 Ω-domain에서 sampling을 계산할 것이다.

# Fourier Transform의 multiplication Theorem

4. Nyquist-Shannon Sampling Thoerem (feat. Aliasing)

(1) Aliasing 

: Baseband signal들의 train이 Sampling과정중에서 Frequency-domain상에서 곂치는 현상

(2) 문제

서로 다른 Analog 신호이더라도, Aliasing에 의해서 Digital 상에서 동일한 신호로 취급된다.

즉, Analog signal 과 Digital signal사이에 1:1 대응이 성립하지 않는 것이다.

결국에는 analog 신호를 ADC,DAC거치고 원본이 아닌 이상한 신호가 나오는 문제점이 발생한다.

(3) 해결방법1  " Nyquist-Shannon Sampling Theorem" 

위 (c)그림에서 Ωs- ΩN이 ΩN보다 크면 된다. 이를  " Nyquist-Shannon Sampling Theorem"  이라고 한다.

즉, 신호의 sampling 속도가 Analog신호의 최대 주파수보다 2배이상은 높아야(sampling이 ㅈㄴ게 빨라야) aliasing이 발생하지 않는 것이다.

(4) 해결방법2 Anti-aliasing

혹은 위처럼 아싸리 Baseband 신호의 고주파 부분을 Ωs/2을 넘지 않도록 짜르는 것도 방법이다. 이를 위해서는 freq-domain에서 Rect(f) function(일종의 filter로 작용)이 필요하다. (즉, time-domain에서는 sinc function에 해당한다....inverse- CTFT)(고주파가 경계에 대응한다.)

이를 이미지 신호 처리상에서 적용하면 고주파신호가 사라지면서 time-domain(이미지에서는 area-domain이라고 해야할까?)에서 이미지가 흐려지는 문제가 있긴하다.

 

5. Sampling된 신호(=x_s(t))를 x_c(nT) (= x[n])으로 변환

(1) 이론적 배경 (DTFT)

- x[n]을 DTFT하면 x(e^jw)이다.

- x_c(t) → x_s(t) by delta-train으로 구성된다.

중요***

- CTFT와 DTFT사이의 관계는 위와 같다.

(참조 : real analysis - What is the relationship between DTFT and continuous fourier transform? - Mathematics Stack Exchange)

(2) x_s(t) → x_c(nT) (= x[n]) 변환

 

- 일단 위처럼 X_s(jΩ)의 공식이 유도된다.

 

 

- 그리고 X(e^jw)를 유도하고 이를 inverse DTFT하는 과정은 위와 동일하다.

 

 

6. Digital Processing(ADC, DAC)

 

 

7. Analog Processing(DAC, ADC)