Notice
Recent Posts
Recent Comments
Link
- 전자과 공대생 블로그(전자회로)
- 전자과 공대생 블로그2(전자기학)
- 배고픈 대학원생 (RF 아날로그)
- 나라발전 교수님 (아날로그)
- [VOD] IDEC 아날로그회로 - 고형호 교수님 (충…
- [VOD] IDEC 아날로그회로2
- [VOD] IDEC 아날로그회로3 - 이강윤 교수님(성…
- [VOD] IDEC 아날로그회로 직관적해석 - 심재윤 …
- [VOD] IDEC 아날로그 LNA - 고형호 교수님 …
- [VOD] Cadence OPAMP Verificati…
- [VOD] IDEC Full-Custom Flow 교육…
- [VOD] IDEC RF System-유형준 교수님(K…
- [VOD] IDEC 디지털 Cell-based 설계
- [VOD] IDEC PLL
- [VOD] IDEC CentOS 7 (Linux)
- [VOD] Band Gap Reference 정리
- [강의] 회로설계 멘토 삼코치
- [강의] OpAmp > CMFB
- [강의] 변박사님 : OpAmp, Radar
합법적사기꾼지망생
전자기학 Ch04.8, Ch05.6 Boundary Condition(경곗값 조건) 본문
A2_전자기학 & 전자장/Fundamentals of Electromagnetics - Ulaby
전자기학 Ch04.8, Ch05.6 Boundary Condition(경곗값 조건)
평범한 민석이 2023. 10. 24. 13:17경계면에 tangent한 성분과 normal한 성분을 나눠서 분석하자(total FIeld는 두 성분의 Linear Combination과 동일하기 대문이다.)
참고로 요약하면 모든 field는 spatially continuous해야한다.
1. Electrical Field (tangen)

flux는 spartially continuous해야해서 위와 같은 공식이 나온다.
2. Electrical Field (normal)

위 법칙은 Gauss 법칙을 참조하면 쉽게 유도할 수 있다.
만약 voltage source가 없다면 우변의 ρ_s를 없애면 된다.
※ 도체와 부도체 사이 경계면에서의 조건

3. Magnetic Field(tangent)

flux는 spartially continuous해야해서 위와 같은 공식이 나온다.
4. Magnetic Field(normal)
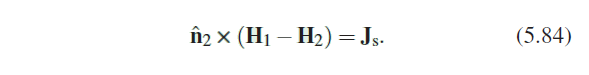
위 법칙은 Ampere법칙을 참조하면 쉽게 유도할 수 있다.
만약 voltage source가 없다면 우변의 J_s를 없애면 된다.
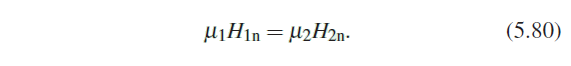
'A2_전자기학 & 전자장 > Fundamentals of Electromagnetics - Ulaby' 카테고리의 다른 글
| 전자기학 Ch07.6 Electromagnetic Power Density (0) | 2023.10.24 |
|---|---|
| E-field, H-field와 ε, μ사이의 관계 (0) | 2023.10.24 |
| 전자기학 Ch07.1 Maxwell Equation → homogeneous Helmholtz Equation = Wave Equation → Plane-Wave (feat. tan δ) (0) | 2023.10.24 |
| 전자기학 Ch01.7 Traveling Waves in the Phasor Domain (0) | 2023.10.24 |
| 전자기학 Ch01.4 Traveling Waves (1) | 2023.10.24 |




