합법적사기꾼지망생
전자장 Ch13.2 Microwave Oscillator (+ Kurokawa's Stable Oscillation Condition) 본문
전자장 Ch13.2 Microwave Oscillator (+ Kurokawa's Stable Oscillation Condition)
평범한 민석이 2023. 7. 31. 17:38기존 발진의 정의 : Bakhausen Criterion, Positive Feedback, K-factor 등등과 비교하면서 생각해보자
(제어공학,전기회로, 전자회로)
사전 내용
RF 회로개념 잡기 - PART 2 ▶ Oscillator (발진기) (rfdh.com)
RF 회로개념 잡기 - PART 2 ▶ Oscillator (발진기)
RF 시스템에 절대로 없어서는 안될 주연배우들 중 하나인 오실레이터(oscillator, 발진기)의 역할과 원리를 이해하고, 발진기란 정확히 '무엇인가'와 '왜 존재하는가?' 에 대한 개념을 잡는 시간을
www.rfdh.com
내용
1. Oscillation의 "전제"조건
(1) Active Device의 존재 유무
(2) Γin >1 혹은 Re{Zin} < 0 (Stabiltiy Circle/Region 참조)
Negative Impedance = 발진 이라고 해석하는 이유는 신호원 = Negative Impedance이기 때문이다.
RF 회로개념 잡기 - PART 2 ▶ Oscillator (발진기) (rfdh.com)
RF 회로개념 잡기 - PART 2 ▶ Oscillator (발진기)
RF 시스템에 절대로 없어서는 안될 주연배우들 중 하나인 오실레이터(oscillator, 발진기)의 역할과 원리를 이해하고, 발진기란 정확히 '무엇인가'와 '왜 존재하는가?' 에 대한 개념을 잡는 시간을
www.rfdh.com
이때 착각하면 안되는 주의사항이있다.
1. Γin > 1 일 때, Γin = Vout-/Vin+ 이다. 이때, Noise가 Vin+의 역할을 수행한다.
2. 하지만, Γin이 더 크다고 더 크게 발진하는 것이 아니다. 오히려 Rin의 절댓값이 큰 것이 훨~씬 중요하다.
3. 위 2개는 충분조건일 뿐이다. 이것을 만족한다고 발진하지는 않는다. 뒷단에서 attenuation이 심하면 발진하더라도 발진하기 전에 신호가 Feedback loop동안 소실되어버리기 때문이다.
2. Microwave Oscillator 설계
(1) 1번에서 말한 발진조건을 아래의 회로에서 구현해보자
이때 발진기 = Active network는 1-Port Network로 해석한다.

(2) 키르호프 공식적용
키르호프 법칙을 적용하고나서 I(Complex Current)가 0 A 가 되지 않으려면 임피던스 성분합이 0이 되어야한다.

이때, 키르호프 공식을 적용하여 steady-state oscillation의 조건(=식 13.25)을 구할 수 있다. [ 그리고 이때, 식(13.25b = 13.31b)는 Resonator의 역할로 추측된다 ]
이를 반사계수로 나타내면 아래와 같다.

하지만 초기 발진조건(start-up)을 포함하려면 13.31과 같은 식으로 변경되어야한다.

이때, Rin과 Xin은 Active Device이기 때문에, Complex Current (I)에 의해 영향을 받는다.
그리고 RL과 XL은 Passive Device이기 때문에, Current(I)에 영향을 받지 않는다.
그리고 Transient 과정중에서 Rin과 Xin, RL과 XL은 모두 변한다고한다.
변화 과정을 읇으면 아래와 같다.
1. I=0(초기조건)으로 시작한다. 이때, Rin(I,jw)는 절대값이 매우큰 음수이다. 노이즈성분에의해 임의의 주파수(w)로 발진을 시작한다. ... Unstable Oscillation
2. I가 점점 증가한다. Rin(I,jw)의 절대값이 감소한다.
3. reactance 성분이 resonator역할을하여서 w=w0 성분만 점점 살아남는다.
4. I가 I0(임계값)에 도달한다. 주파수도 w0로 도달한다. .... Stable Oscillation

(3) S11>1이면 발진할 수 있는 이유(Unstable)(≠oscillation)
: V_+가 S_11으로 인해서 V-이 되고 [V- = V_+ × S_11]
: V_-이 source matching stage에 의해서 Γs로 되돌아온다. [V_+ = V_- × Γs]
: 그러면 Black Box의 Input 쪽에 수많은 신호들이 등비급수의 형태로 합해진다.
: 이때, 등비가 S_11 × Γs이므로 S_11이 충분히 1보다 크면 발진하는 것이다. (이러한 분석은 아래의 식에 반영)

: 위와 같은 분석은 Oscillator의 "Core단의 Negative Impedance"와 "Resonator단의 Q-factor(ex. LC Tank)"에 의해서 결정된다.
: 물론 이때 S_11 × Γs의 위상이 360º × n(positive feedback)이면 발진을 더 잘할 것이다. (이러한 분석은 아래의 식에 반영)

참조 : Oscillation Explanation using S-parameters | Forum for Electronics (edaboard.com)
Oscillation Explanation using S-parameters
Im designing a microwave oscillator using an S2P file. Because of this linear model, I cannot do any nonlinear analysis, so I'm stucked with the S-parameter output. How can I know if my oscillator is oscillating? My adviser told me that if S11>1, my oscill
www.edaboard.com
3. Stable Oscillation 이란?
주파수나 Power(Current에 비례)가 변하여도 원래의 주파수 및 전력으로 돌아오는 발진. 즉 steady-state가 존재하는 발진. 이를 위해서는 Kurokawa의 조건을 만족해야한다.
4. Kurokawa's Condition for Oscillation
(1) 유도과정
전류의 진폭(I)가 증가함에따라 Total Resistance(R)의 변화는 아래와 같다.

우선 회로(발진기)가 Stable Oscillation 하기 위해서는 I_0, w_0(※ s_0=jw_0) 인 지점에서(=steady-state, stable oscillation) Total Impedance가 0이 되어야한다. (위 그래프 참조) 이를 식으로 적으면 아래와 같이 표현될 것이다.


Stable Oscillation이라면 위 식에서 당연히 첫째 항은 사라질 것이다.

Stable Oscillation이라면 위 식에서 당연히 둘째 항은 아래와 같이 표현된다.

이때, 둘 째 항의 δs는 아래와 같이 정의된다.

식 13.28을 13.27의 2째항에 대입하여 식을 정리하면 아래와 같다.

(2) Kurokawa Stable Oscillation Condition의 정리
Stable Oscillation의 조건은 아래와 같다.

위 수식을 Kurokawa's condition 이라고한다. (발진조건아니다. Stable 발진 조건이다.)
이에 따르면 Q factor가 높을수록 Oscillation의 Maximum Stability를 가져갈 수 있다고 한다. 그래서 공진기 (Cavity, Dielectric)등이 사용되는 것이다.
하지만 위 식은 직관적이지 않으므로 좀 더 추려 보자.
(3) Kurokawa Stable Oscillation Condition의 의의
Kurokawa Condition을 다시 정리하면 위와 같다.
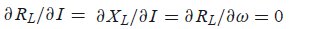
이때, RL과 XL은 진폭에 무관하다. 특히 RL은 주파수에도 무관하다고 할 수 있다. 그러면 위의 식을 식13.29에 대입할 수 있다. 그 결과는 아래와 같다.

그리고 일반적으로 아래의 부등식은 당연히 만족된다.
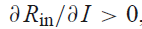
그러면 부등식을 만족시키기위해서 아래의 조건이 만족되어야한다.

즉, Total Reactance의 w에대한 기울기가 양수 이어야한다는 것이다.
그렇지 않는다면 발진을 하더라도 Stable하지 않은, Random 발진이 발생하는 것이다.

(4) (직렬, 전류) 발진기 설계조건
최종적으로 발진기 설계의 조건이 1개 더 추가된 것이다.

https://tgs05016.tistory.com/manage/newpost/892?returnURL=https%3A%2F%2Ftgs05016.tistory.com%2Fentry%2F912-%EB%B0%9C%EC%A7%84Oscillation%EC%9D%98-%EC%A2%85%EB%A5%98-%EB%B0%8F-%ED%8C%90%EB%B3%84-One-port-point-of-view%EC%9D%98-%ED%99%95%EC%9E%A5Razavi-Pozar-%EC%86%8C%EC%8B%A0%ED%98%B8-%EB%8C%80%EC%8B%A0%ED%98%B8-%EA%B4%80%EC%A0%90&type=post
tgs05016.tistory.com
5. 추가변수
1. stable operation
2. maximum power output
3. frequency pulling
4. injection locking(range)
5. large-signal effects
6. noise characteristics
의문점
그렇다면 Rs=-Rin/3 (식 13.31a)을 만족시키는 주파수대역에서 (식 13.31b)를 만족시키지 않으면 어떻게 될까? 주파수와 진폭이 거의 랜덤하게 바뀌는 신호가 회로에서 측정된다.(쓰래기 회로)
9.0.3 Stable Oscillation(정상상태발진) vs. Unstable Oscillation 발진이 개!같은 이유 (tistory.com)
9.0.3 Stable Oscillation(정상상태발진) vs. Unstable Oscillation 발진이 개!같은 이유
1. Stable Oscillation(정상상태발진) 정상상태 발진은 한개의 주파수로 일정한 진폭을가지면서 sin파가 만들어지는것이다. 이런경우 다음의 규칙을 만족한다. 이를 위해서는 아래의 LoopGain발진조건에
tgs05016.tistory.com
----------------------------------------------------------------- 광 고 -----------------------------------------------------------------
'A2_전자기학 & 전자장 > Microwave Engineering - Pozar' 카테고리의 다른 글
| Q) 전송선이론 vs. 소신호모델(+키르호프 법칙) : 뭐가 맞는 이론일까? (0) | 2023.08.16 |
|---|---|
| 전자장 Ch12.4 Broadband Amplifier Design 방법들(Balanced, Distributed, Neutralization, Double-peaking, Staggery, Q-factor) (3) | 2023.07.31 |
| 전자장 +α) S-parameter와 Harmonic Balance 차이 (0) | 2023.07.30 |
| 전자장 Ch10.2 Nonlinearity 공식 정리(feat. P1dB 공식)** (0) | 2023.06.22 |
| 전자장 Ch12.1+α : 증폭기의 Gain, Power 공식 총정리***** (0) | 2023.06.22 |



