- 전자과 공대생 블로그(전자회로)
- 전자과 공대생 블로그2(전자기학)
- 배고픈 대학원생 (RF 아날로그)
- 나라발전 교수님 (아날로그)
- [VOD] IDEC 아날로그회로 - 고형호 교수님 (충…
- [VOD] IDEC 아날로그회로2
- [VOD] IDEC 아날로그회로 직관적해석 - 심재윤 …
- [VOD] IDEC 아날로그 LNA - 고형호 교수님 …
- [VOD] Cadence OPAMP Verificati…
- [VOD] IDEC Full-Custom Flow 교육…
- [VOD] IDEC RF System-유형준 교수님(K…
- [VOD] IDEC 디지털 Cell-based 설계
- [VOD] IDEC PLL
- [VOD] IDEC CentOS 7 (Linux)
- [VOD] Band Gap Reference 정리
합법적사기꾼지망생
통신 Ch02. Fourier Series(CTFS, DTFS) & Fourier Transform(CTFT) 본문
통신 Ch02. Fourier Series(CTFS, DTFS) & Fourier Transform(CTFT)
평범한 민석이 2023. 8. 27. 21:490. Fourier Series란? (자체필기)
추가참고자료 BOS의 스터디룸
(77) [푸리에급수] 1편. 직관적인 소개 ('푸리에 급수'란 , sin급수 cos급수 전개) - YouTube
위 영상을 보고 오면 도움이된다. (공학수학 관점에서 Fourier Series 해석)




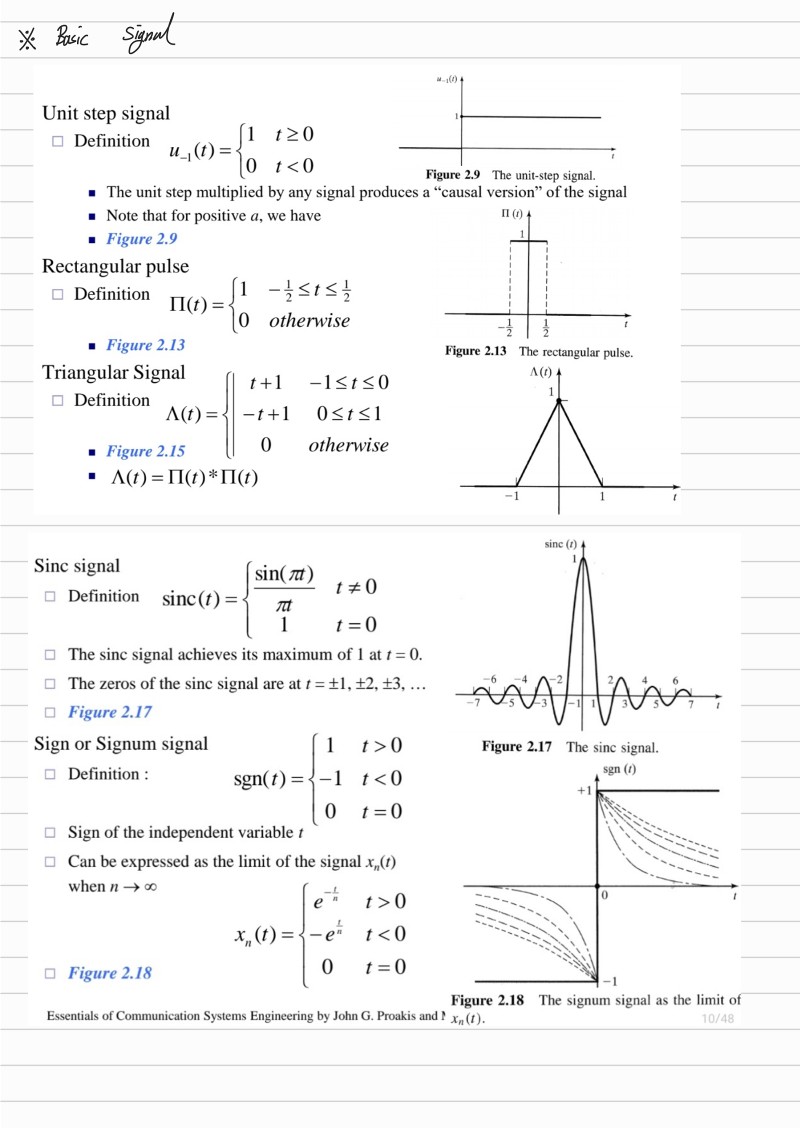
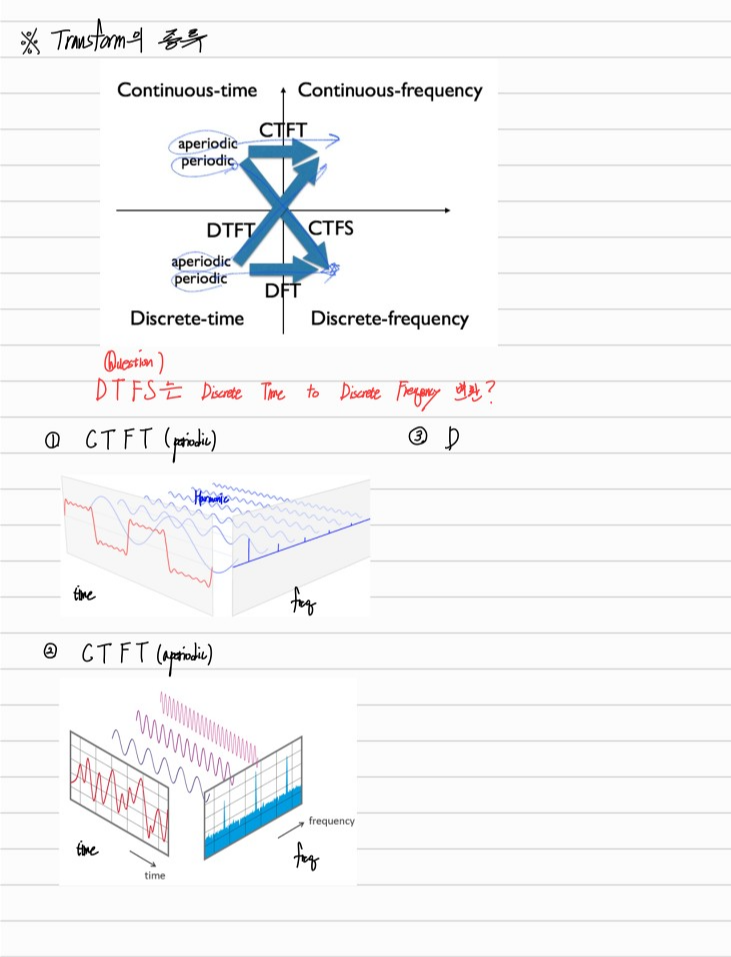

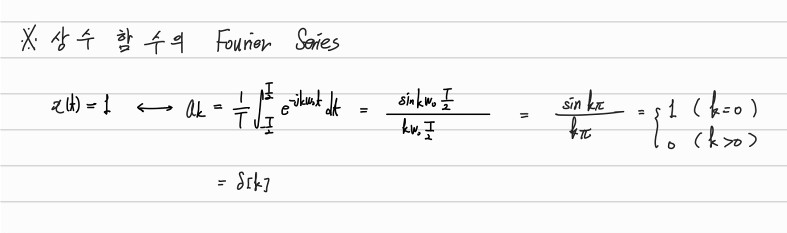



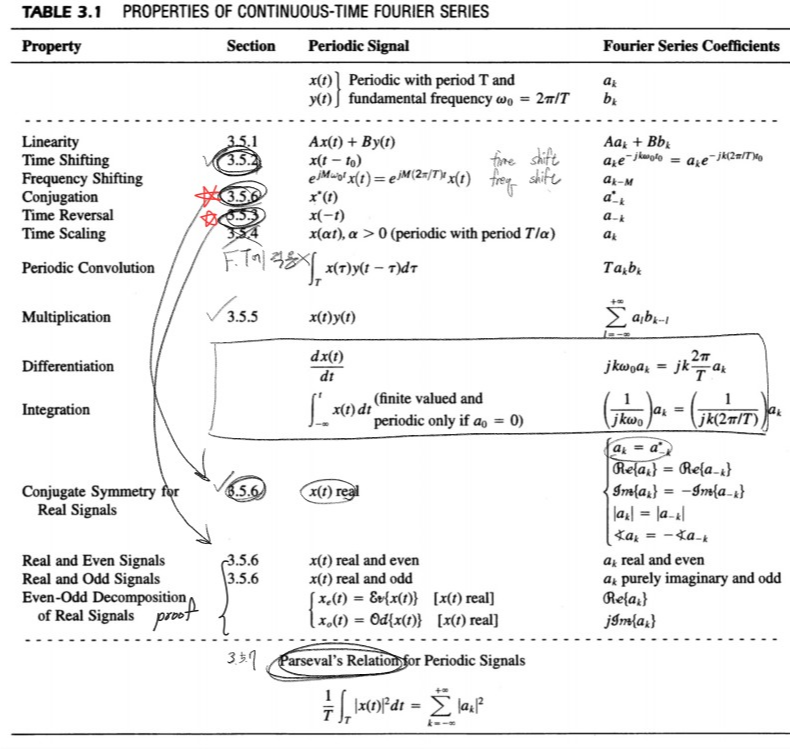



1. Fourier Transform 이란? 분류? 비슷한 다른 Transform?
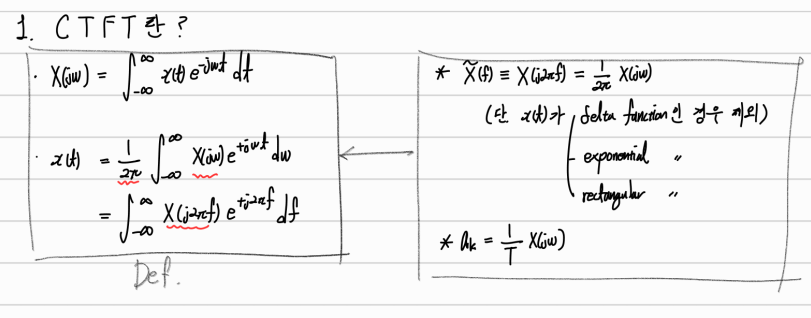
(0) 정의 : Time Domain 신호를 Frequency Domain에서 표현한것
: 사실 Delta fucntion이 Basis라서, Impulse Representation을 했듯(time domain),
: Complex Exponential Fucntion 또한 Basis에 해당되어서, Fourier Representation으로 나타낼수 있다.(Frequency domain)
*참고로 모두 선형 변환에 해당한다.(선형대수학 참조)
(1) CT
CTFS : Periodic SIgnal & Continous Time Domain → Discrete Frequency Domain
CTFT : Aperiodic Signal & Continouse Time Domain → Continous Frqeuency Domain(frequency reponse)
Laplace Transform : CTFT의 확장, 복소 주파수 (transfer function)
(2) DT
DTFS : Periodic SIgnal & Discrete Time Domain → Discrete Frequency Domain
DTFT : Aperiodic Signal & Discrete Time Domain → Congtinous Frequency Domain(frequency response)
Z-Transform : DTFT의 확장, 복소 주파수 (system function)
DFT : Aperiodic Siganl & Discrete TIme Domain → Discrete Frequency Domain
2. CTFS이란??
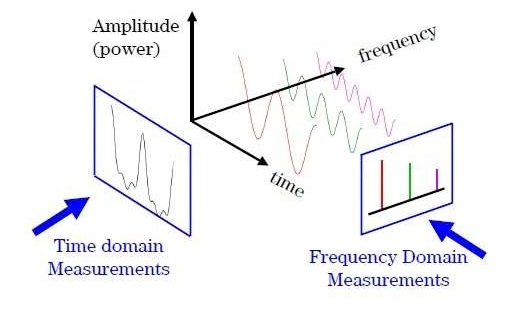
모든 주기함수는 Sin 및 Cos 함수의 합으로 표현할 수 있다.
3. CTFT이란?
비주기함수 또한 주기(T)가 무한히 큰 주기함수로 보고 CTFS할 수 있다.
4. CTFT가 중요한 이유? : Frequency Response
(1) 주파수에 따른 분석의 용이(Gain의 곱셈이기 때문에. 곱셈인 이유는 (2)번 참조)
: 미리 말하자면 이것만 기억하자
Gain은 곱해지고 Phase는 더해진다.
(2) Impulse Response와 Frequency Response는 CTFT관계에 있다.
(3) Time-domain의 Convolution 연산은, Frqeuency Domain에서 곱셈에 해당된다.
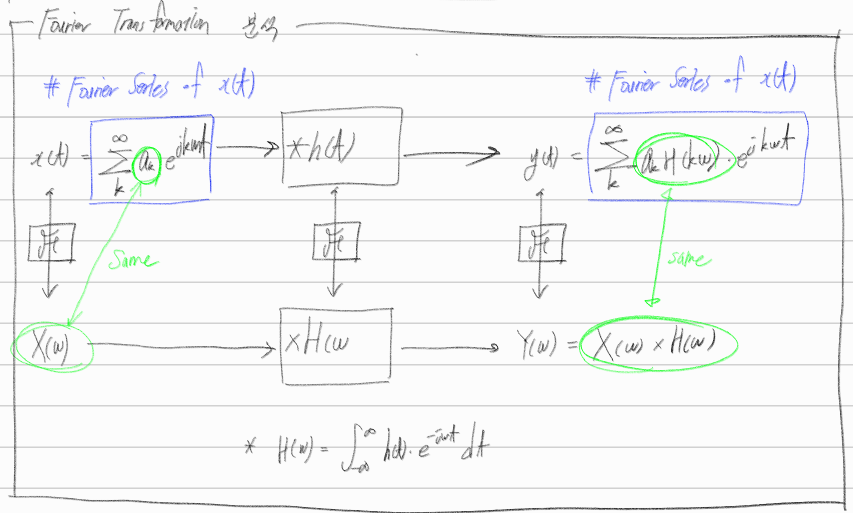
5. CTFT 공식들



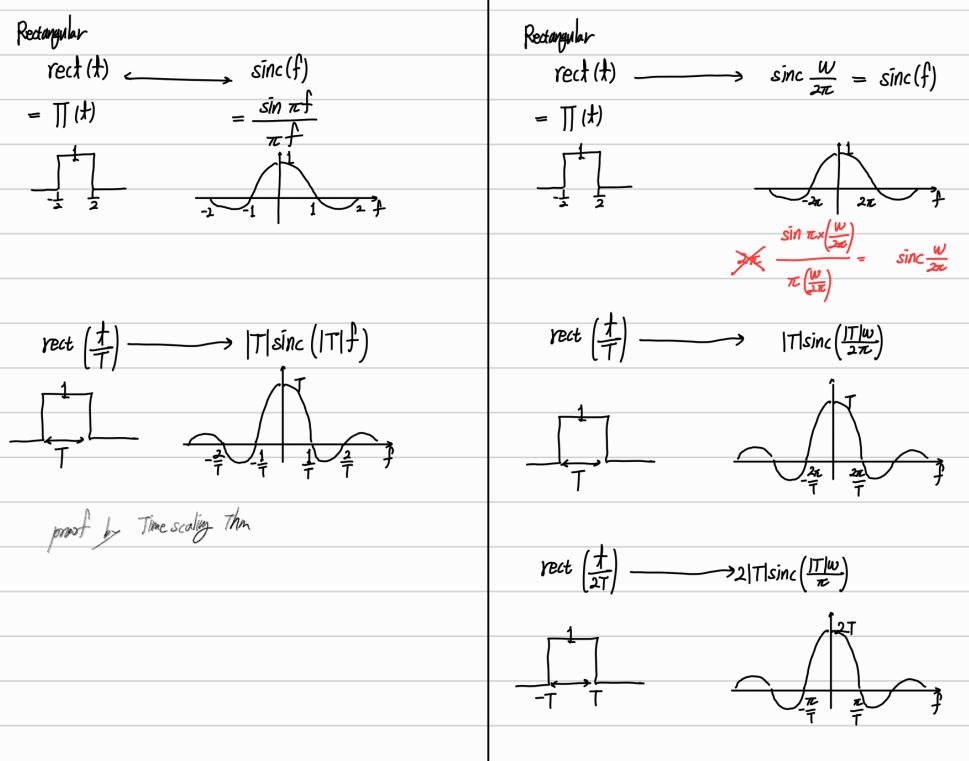
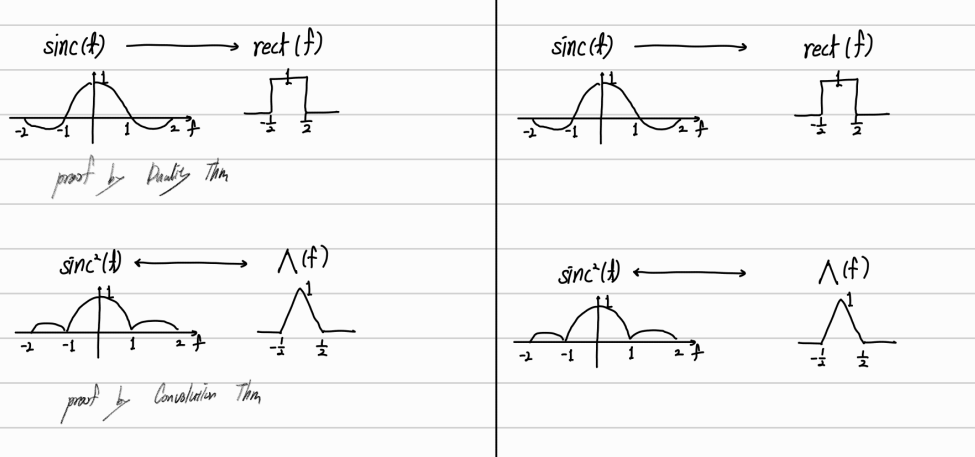
'C1_Analog Communication > Signal and System & Analog Communication' 카테고리의 다른 글
| 통신 Ch03. Analog Modulation(AM,FM,PM) (0) | 2023.08.30 |
|---|---|
| 통신 Ch02 + α. Hilbert Transform(feat. SSB AM) (0) | 2023.08.30 |
| 통신 +α . Sinc Fucntion과 Rect Fucntion의 CTFT관계 (0) | 2023.08.28 |
| 아날로그 통신이론 목차 (0) | 2023.08.27 |
| 통신 Ch01. Signal and System : ~ Impulse Response(LTI) (0) | 2023.08.27 |



