- 전자과 공대생 블로그(전자회로)
- 전자과 공대생 블로그2(전자기학)
- 배고픈 대학원생 (RF 아날로그)
- 나라발전 교수님 (아날로그)
- [VOD] IDEC 아날로그회로 - 고형호 교수님 (충…
- [VOD] IDEC 아날로그회로2
- [VOD] IDEC 아날로그회로3 - 이강윤 교수님(성…
- [VOD] IDEC 아날로그회로 직관적해석 - 심재윤 …
- [VOD] IDEC 아날로그 LNA - 고형호 교수님 …
- [VOD] Cadence OPAMP Verificati…
- [VOD] IDEC Full-Custom Flow 교육…
- [VOD] IDEC RF System-유형준 교수님(K…
- [VOD] IDEC 디지털 Cell-based 설계
- [VOD] IDEC PLL
- [VOD] IDEC CentOS 7 (Linux)
- [VOD] Band Gap Reference 정리
- [강의] 회로설계 멘토 삼코치
- [강의] OpAmp > CMFB
- [강의] 변박사님 : OpAmp, Radar
합법적사기꾼지망생
전자장 Ch12.2 Stability(안정도) of Amplifier : Stability Circle, Stability Factor (정독필수) 본문
전자장 Ch12.2 Stability(안정도) of Amplifier : Stability Circle, Stability Factor (정독필수)
평범한 민석이 2023. 6. 1. 19:13
위 회로가 발진(Oscillation)하지 않기위해서는 어떻게해야할지 알아보자.
우선 의식의 흐름대로 1~4로 구성되었음을 독자들에게 알린다.
주의사항 : 아래의 내용들은 Large-Signal Regime에서는 적용이 불가능하다. 거기서부터는 Pole-zero Identification(제어공학의 내용)을 적용해야한다.
참조 : Diapositive 1 (amcad-engineering.com)
내용
1. 발진(Oscillation) : 안정(Stable)의 반대? No
Oscillation ⊂ Unstable ↔ Stable
(1) 음수 입력 임피던스
: 이는 Smith 차트에서 단위원 밖을 의미한다.
(2) Closed Loop System에서 분모가 0 : Barkhausen criteria
(3) Positive Feedback
(4) s-plane상에서 Left Half Plane(LHP)에 Pole이 존재
참조
전자장 Ch13.1.0 Stability/Oscillation Criteria 총정리(전자회로,제어공학,전자장) (tistory.com)
2. Unconditional Stability vs. Conditional Stability
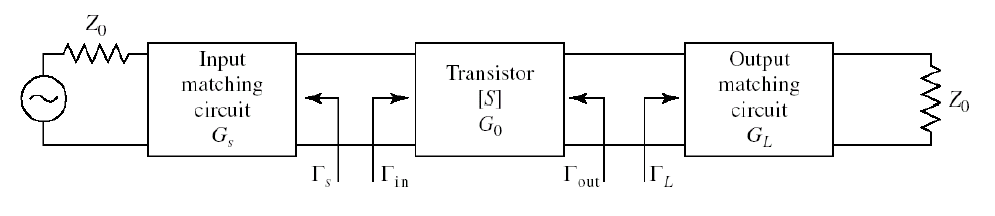
(1) Stable Condition
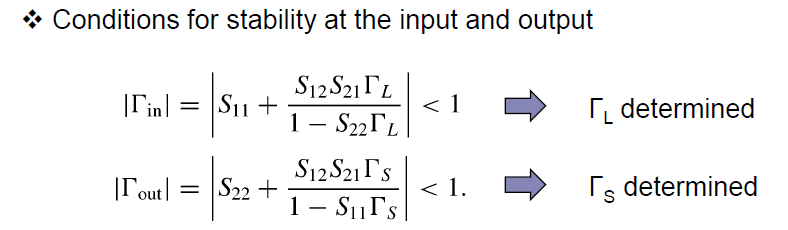
(2) Unconditional Stability
Γs와 ΓL에 무관하게, Γin<1 && Γout <1
(3) Conditional Stability
Γs와 ΓL값에 따라서, Γin<1 && Γout <1
(4) Potential Unstable
Γin(=S11)>1 || Γout(=S22) >1 when ΓL=0, Γs=0
3. Stabiltiy Circle
: Stable Condition의 경계지점을 원으로 표현하자(Locus of ΓL and Γs)
: (착각하기 쉬운 것) 해당글에서 Stability Circle은 Smith Chart 상에서 그릴 것이라고 배울 것이다. 그런데 Stability Circle은 어떤 반사계수 or S-parameter에 해당하는 Smith Chart에 그리는 것일까?
해당 챕터에서는 독립변수역할을 하는 것이 바로 Γs와 ΓL이다. Γs와 ΓL가 변함에 따라 Γin=1 혹은 Γout =1이 되는 지점의 Contour를 그릴 것이다. 즉, 해당 Circles(Source Stability Circle, Load Stability Circle)은 각각 Γs-plane과 ΓL-plane에 그려진다.
(1) Input Stability Circle(= Load Stability Circle ): 2-Port Network에서는 ΓL에 의해서 Input Oscillation이 발생한다. (반대로, Γs에 의해서 Output Oscillation이라 발생하고 그 임계지점을 Output Stabiltiy Circle(=Source Stability Circle)이라고 표현한다.)
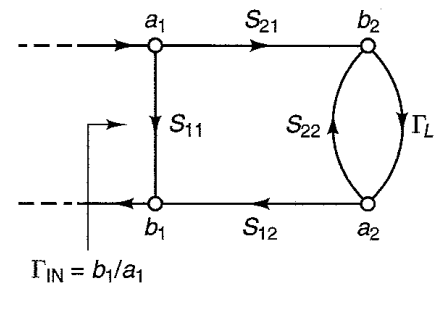
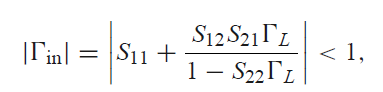
Input Stable Condition은 위와 같고, (독립변수 ΓL)
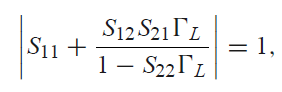
경계지점은 위와같이 표현이 가능하다(부등식을 방정식을 바꿈)
그리고 위 식을 쭉 전개하면 아래와 같이 된다.
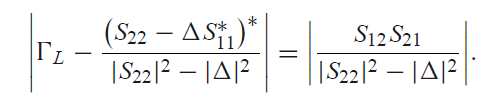
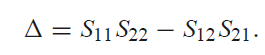
위 식의 양변을 제곱하면, ΓL에 대한 원의 방정식이다. △은 scattering matrix의 행렬식(determinant)이다.
원의 중심(CL)과 반지름(RL)은 다음과 같다.
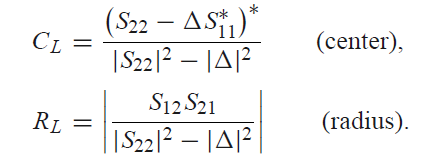
이 원은 Γin에 그려진다.
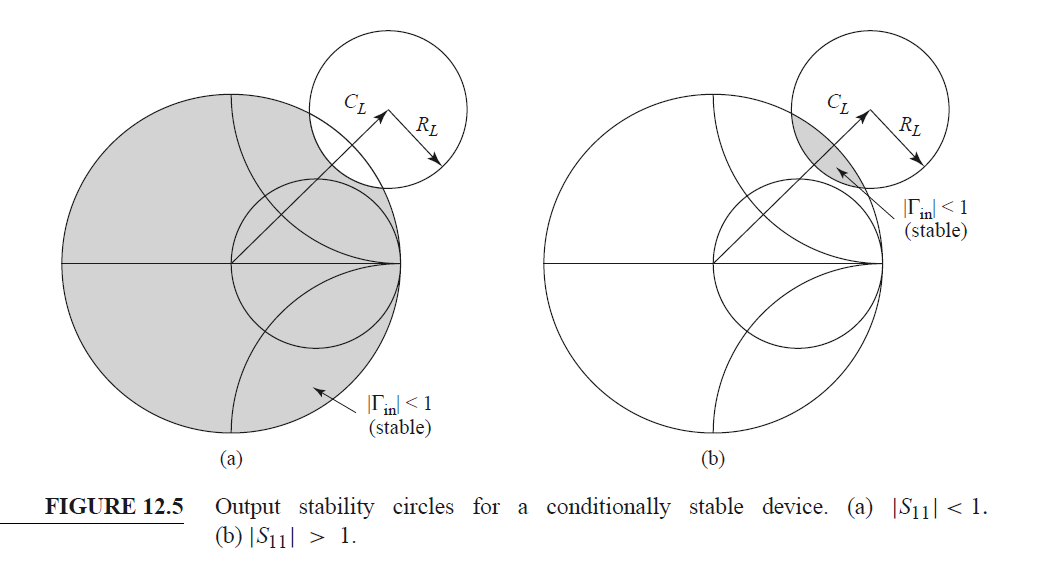
그리고 S11이 대부분 1보다 작기 때문에 (a)처럼 Stable Region이 형성된다.
그리고 위 스미스차트는 ΓL의 Polar Chart이다.(Locus라는 자체가 ΓL에대한 원방정식으로 유도되었으니까)
주의사항
절대로, S(1,1)<1이면 Stability Circle내부가 Stable Region이고 S(1,1)>1이면 Stability Circle외부가 Stable Region이라고 이해해선 안된다!!!!!!!!! Stability Circle은 그저 Stable영역과 Unstable영역 사이의 Boundary역할을 할 뿐이다. 오로지 스미스차트의 원점이 stable region인지 여부를 판단하는 근거로 S(1,1) <1 부등식을 적용해야한다.
좀 더 자세히 설명하자면
S(1,1)이라는 것은 사실 "Load Port가 50옴일 때(ΓL == 0 ), Γin의 값의 크기< 1"을 의미한다.
S(1,1)<1이라는것은 ΓL-Plane상(스미스차트)에서 원점을 포함하는 영역이 Stable Region for Output이라는 뜻이다!!!
반대로,
S(2,2)<1이라는 의미는 "Source Port가 50옴일 때(ΓS== 0 ) , Γout의 값의 크기 < 1"을 의미한다.
S(2,2)<1이라는 것은 ΓS_Plane상(스미스차트)에서 원점을 포함하는 영역이 Stable Region for Input이라는 뜻이다.!!!
이의 경우에는 아래의 그림 설명을 참조하자

참조
Understanding Stability Circles (highfrequencyelectronics.com)
Understanding Stability Circles
www.highfrequencyelectronics.com
(688) Lecture 12.3 - Stability, the traditional way... - YouTube
(2) Output Stabiltiy Circle(=Source Stability Circle)
앞선 내용과 마찬가지로 Source에 의해서 Output이 발진할 수 있다. 그러므로 Output Stability CIrcle은 Γs-plane상에서 그려진다.
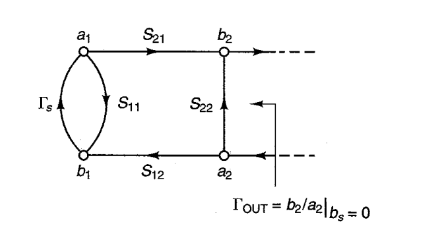
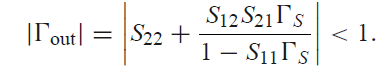
Output Stable Condition은 위와 같고, (독립변수 Γs)
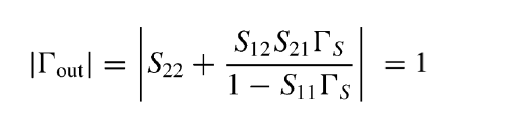
경계지점은 아래와 같이 표현이 가능하다
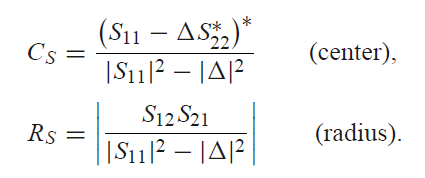
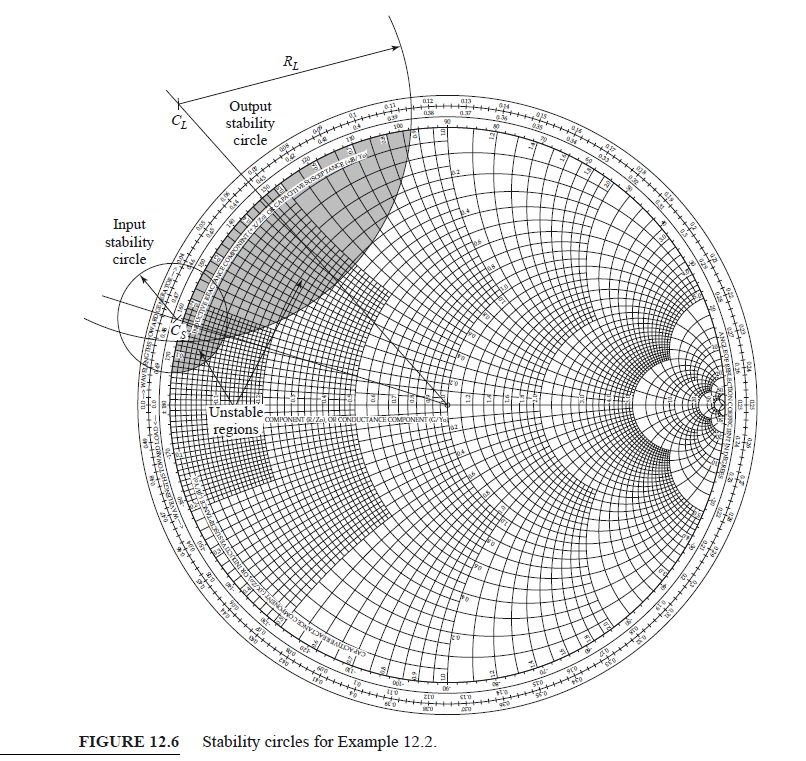
위 스미스차트는 Γout의 Stability Circle과 Γin의 Stability Circle을 Γs, ΓL Plane 상에서 각각 나타내어 곂친 그림이다.(Locus라는 자체가 Γs, ΓL에 대한 원방정식으로 유도되었으니까)
그리고 ΓL와 Γs은 위의 Figure 12.6처럼 한개의 Polar Chart(겸 Smith Chart)에 나타낼 수 있다.
주의사항!!! 꼭 기억할것
1. Output Unstable Region을 Source Impedance가 침투하는지 확인하는 방법
Γs의 S-parameter와 Γout의 Stability Circle는 서로 다른 Smith Chart에 그려진다.
(둘 다 ADS 및 Virtuoso Tools 상에서 S(1,1)-plane 상으로 표현되지만, 각각 Γs, Γout-stability circle으로써 서로 다르다. 전자는 Input Matching Stage의 Output을 바라본 값(=Γs)이고, 후자는 Device의 Input(=S11 of Device)을 바라본 값이다.)
(말이 이해하기 어렵네, 인터넷에서 검색해보라. 나도 설명을 나중에 가다듬을테니)
그리고 이때 두 그래프를 겹쳐서 보면서 각각의 주파수에 대해서 Γout의 Unstable Region을 Γs의 S-parameter가 침범하는지 확인하면 된다.
(이때, Device의 Γs S-parameter(=S11)를 반드시 참조해야한다. Stable Region이 Stability Circle 내부인지 외부인지 확인해야하기 때문이다.)
2. Input Unstable Region을 Source Impedance가 침투하는지 확인하는 방법
위와 동일한 방법으로,
Γin의 Stability Circle의 내/외부를 ΓL의 S-parameter.가 침범하는지 확인하면 된다.
(Γin의 1보다 큼/작음을 기준으로 Stability Region이 Stability Circle의 내부 혹은 외부를 판별)
의문사항???
1. Maximum Stable Gain은 Stable을 벗어나기 직전의 Gain을 의미한다.??
즉 MSG를 넘어가면 발진한다는 뜻일까??
그렇다면, MSG를 넘어가지 않으면 Stable하다는 뜻일까??
즉, MSG을 넘은 Γs와 ΓL의 위치는 UnStable Region 상에 있다고 생각하면 되는것일까? (모르겠다.)
(1) 찬성
맞는것같다 위 이상의 Gain을 얻지않으면, Conditionally Stable이라고한다. (참조 참고)
(2) 반대
MSG는 MAG에서 k=1을 대입한 것일 뿐이다.
2. Nyquist Stability Criterion과 Stable Circle을 통한 Stability 판별은 서로 "필요충분"조건 일까?
(예시가 Amp 카테고리에 있다.)
추가적인 주의사항
Negative Impedance가 보인다고 무조건 발진하는 것은 아니다.!!!!!!!!!!!!
아래의 링크 참조
4. Parameters for Unconditional Stability, Relative Stability
(1) K factor , K-△ test (Rollet's Stability Criterion = Kurokawa Stability factor = Stern Stability factor)
Stabiltiy Circle의 반지름이 원의 중심부터 원점까지의 거리보다 크다면 어떻게 될까?
당연히 Stability Circle이 Smith Chart(반지름1)밖으로 나갈 것이다.
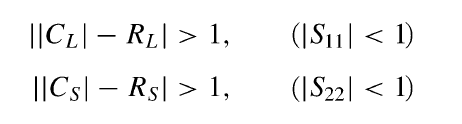
앞선 Stabiltiy Circle의 중심 및 반지름 식에서 착안하여 아래의 변수를 유도할 수 있다.
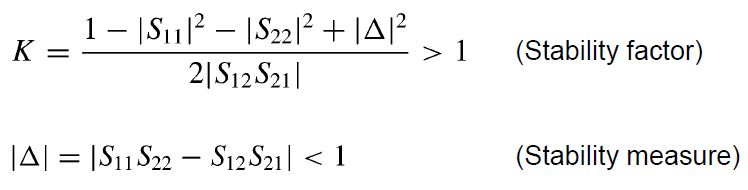
K-factor는 1보다크면 시스템이 무조건 안정함을 보장한다
하지만 K는 상대적인 비교가 아예 불가능하다
예를들어 K=10인 시스템과, K=1000인 시스템 중에서 뭐가 더 안정적이라고 말할 수 없는것이다.
(그런데, Rollett 논문에 보면 상대적인 비교가 가능하다고 나와있음. 누가 틀렸을까?)
*참조) 시뮬레이션: K도 주파수에 따라서 sweep이 가능하다
참고로 Rollett Criterion 을 쓸려면 Intrinsically Stable한 시스템, 즉, Input/Output Impedance가 Postive Resistance를 각각 갖고 있을 때에만 적용이 가능하다.
(내생각인데) Rollett Criterion 을 쓴다는 것은 50 Ohm port가 연결된 I/O 지점에서 (모든 Γs'과 ΓL'에 대해서) Γin'(≠Γin)과 Γout'(≠ Γout)이 1보다 작다는 것을 의미한다. 하지만 내부에서 발진이 일어나는지 아닌지를 판별하는 기준이 될지는 논의가 필요하다(나는 개인적으로는 아니라고 생각한다.)
Stability and Power-Gain Invariants of Linear Twoports | IEEE Journals & Magazine | IEEE Xplore
주의사항 : k>1이라는 분석은 다음과 같은 전제조건하에 설계된다.
1. Input/Output Matching Stage는 오로지 Passive 소자로만 구성된다.
:그래야만 Γs와 ΓL<1 을 언제나 만족한다. (Active 소자는 Γ가 단위원(반지름이 1인원) 밖으로 나갈 수 있다.
2. 2-port Network라는 전제
3. 소자 내부 발진이 없다는 전제
그러므로 Cascode, Multi-stage Amplifier의 경우 k로 분석하는 것은 옳지 않다.
출처 : Crippse - RF Power Amplifier for Wireless Communications
※ Rollett Proviso : k-factor을 쓰기전에 전제조건
: Linear 2-port System 이어야 한다. (Large Signal Regime 분석을 하려면 Pole Zero Identification(제어공학>Nyquist Stability Criterion을 적용해야한다.)
: Source/ Load Matching 단은 Passive 소자로만 이루어져야한다.
: 양쪽이 Open/ Short일때도 Stable한 시스템이어야한다. 왜냐하면 Rollett Stability Criterion 공식의 원본을 찾아보면 아래와 같은데, z,y,h,g parameter을 정의할 때 한쪽 포트를 Short 혹은 OPEN 시키고 정의하기 때문이다. 그리고 이는 "각각의 포트에서 볼수 없는 unstability를 만드는 internal loop of signal이 없다"는 것과 동일한 말이다.(필요충분조건관계)
(in English, In order to be applicable, the linear two-port must be stable, when both ports are loaded with open and short circuits. This is equivalent to say that the two-port does not have any unstable internal loop whose dynamics is not observable at the ports)

※ 참고로 Open, Short에서 반사계수는 1혹은 -1이다. 즉, 신호가 "전반사"된다. 이때도 Stable해야 진짜 Stable System이라고할 수 있는 것이다. 그리고 Rollet Proviso를 확인하려면 어쩔 수 없이 Pole-zero Analysis를 해야한다.
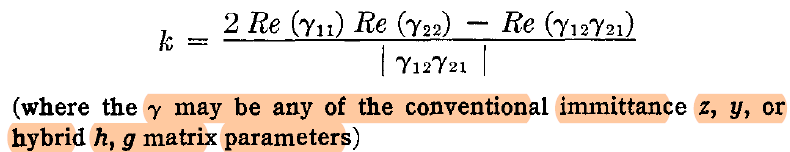
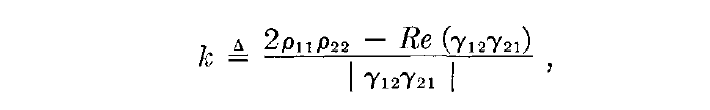
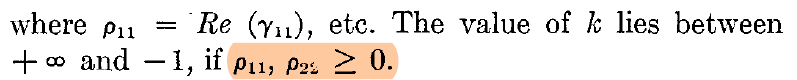
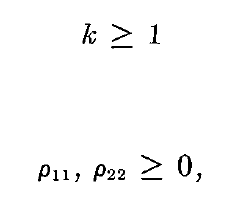
: 즉, 2-port Network 자체적으로 negative resistance 가 보이면 안된다.(이는 원문에도 나와있다.)
: k-factor을 적용하면안되는 예시1
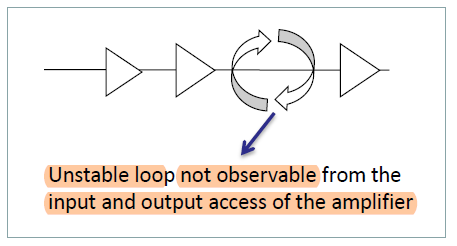
: k-factor을 적용하면안되는 예시2
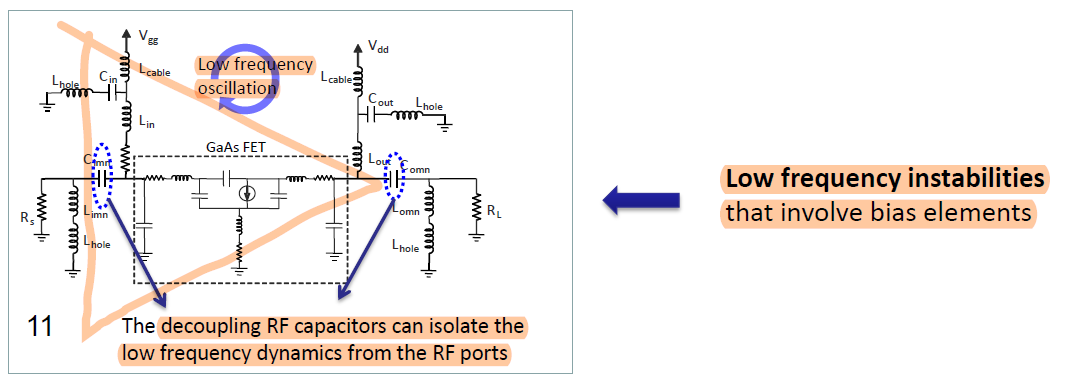
: k-factor을 적용하면안되는 예시3
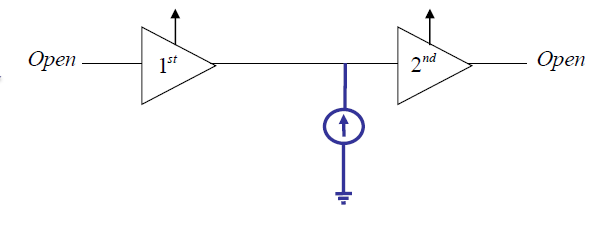
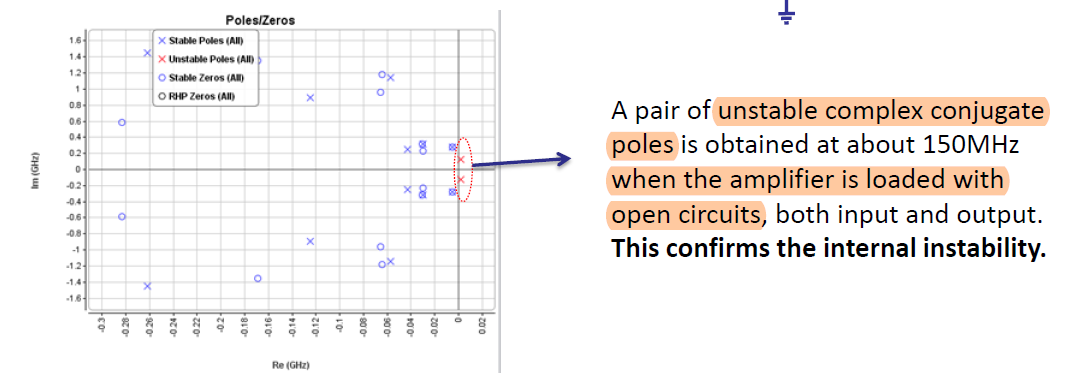
정리 : k-factor 분석 vs. Pole Zero Analysis(Loop Gain Analysis)
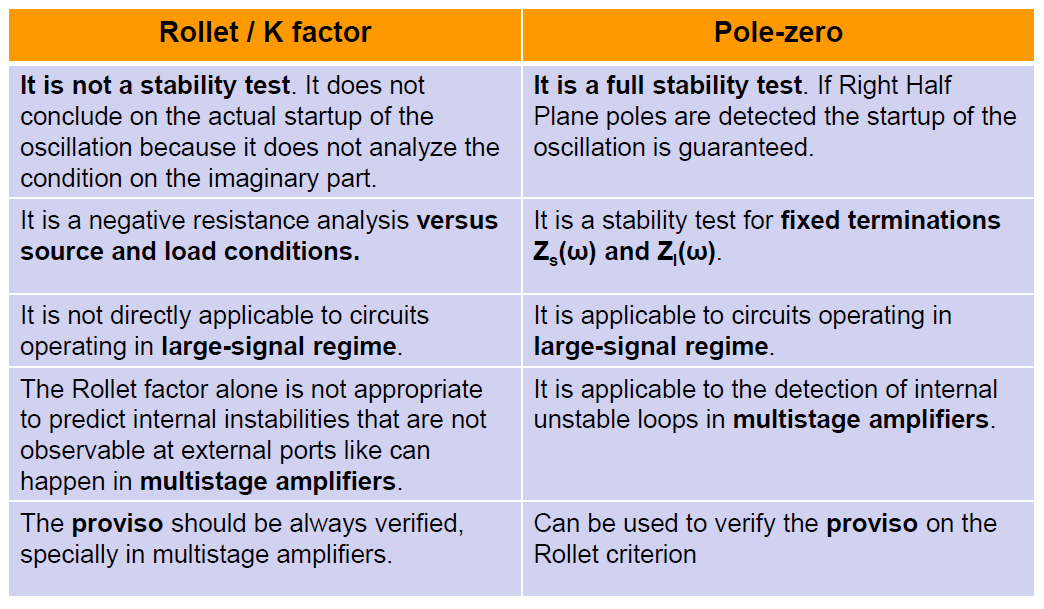
참조 : Diapositive 1 (amcad-engineering.com)
Stability Analysis of RF Power Amplifiers - Amcad Engineering (amcad-engineering.com)
(2) μ factor (Edwards-Sinsky Stability Criterion , Geometric Stability Factor)
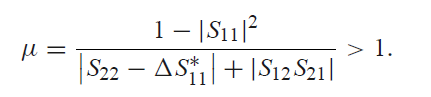
μ>1 && μ'>1 이면 K factor와 마찬가지로 무조건적 안정한 시스템이다.
다만 μ는 K와 다르게 크면 클수록 안정적인 시스템이다.
왜냐하면, 위 Mu라는 수식은 Smith Chart(Source Impedance의 Smith Chart이다.)의 중심으로부터 가장 Unstable한 가능성이 있는(Smith Chart 중심에 가장 가까운 ) 지점까지의 거리를 의미하기 때문이다.(이때, Stability Circle은 Input Impedance의 Smith Chart상에서 그린다.) 그래서 1보다 크면 (Smith Chart의 반지름이 1이라서) Stable하다는 것이다.
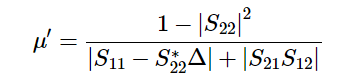
위의 수식은 Mu의 Dual 공식에 해당되며, Output과 Load사이의 Stability를 다루고 있다.
(참고로, ADS라는 EDA에서는 mu와 muprime의 source/ load가 반대로 정의되어있다)
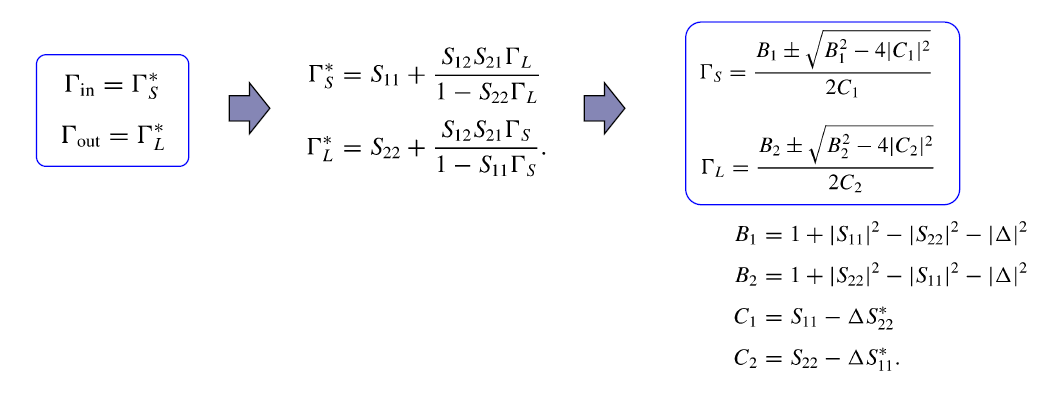
(3) K factor의 의의 : K>1이어야 input&Source과 output&Load의 Conjugate matching이 동시에 가능하다

위식에서 만약 K<1이면 MAG가 존재하지 않음을 알 수 있다. 이는 Simultaneously I/O conjugate Matching이 불가능함을 의미한다.
※ 참조 : Simultaneously Conj matching이란?
(3) B1f (Stability Measure in ADS) (alternative Stability Factor in Virtuoso)

즉,
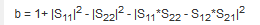
K대신 쓰는 alternative stability factor이다.
참조 : Gonzles Microwave Trnasistor Amplifier, 2nd ed
//Stability Factor and Measure - Stability Factor and Measure - Keysight Knowledge Center
Stability Factor and Measure - Stability Factor and Measure - Keysight Knowledge Center
작성자 : Greg Miller - 8월 20, 2008 Stability Factor (K), Stability Measure (B1) The "Stability Factor and Measure" parameters are real functions of frequency and are available for 2-port networks only. These parameters aid in determining the stabili
docs.keysight.com
(4) Nyquist Stability Criterion
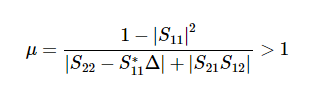
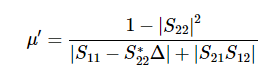
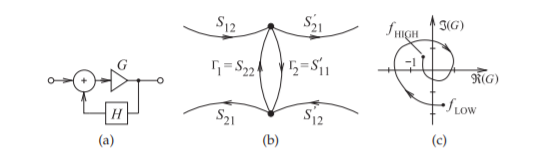
참조 : Pozar교재, 2.6: Amplifier Stability - Engineering LibreTexts
2.6: Amplifier Stability
eng.libretexts.org
Microwaves101 | Stability factor(MSG= Maximum Gain of Conditionally Stable Gain)
Microwaves101 | Stability factor
Home Encyclopedia Calculators Downloads Acronyms Discussion Board Links News Contact Filter by alphabets Filter by categories All1-9ABCDEFGHIJKLMNOPQRSTUVWYZ close Stability factor Click here to go to our page on Normalized Determinate Function (NDF) (new
www.microwaves101.com
----------------------------------------------------------------- 광 고 -----------------------------------------------------------------
'A2_전자기학 & 전자장 > Microwave Engineering - Pozar' 카테고리의 다른 글
| 전자장 Ch12.3.1 LNA의 기본적인 설계 > Source Pull, fT와 NF사이 관계 (0) | 2023.06.01 |
|---|---|
| 전자장 Ch10.1 Noise에 대해서 총 정리 (0) | 2023.06.01 |
| 전자장 Ch12.1.2 Average Transistor Input Power 구하기 (0) | 2023.06.01 |
| 전자장 Ch12.1.1 Input Matching stage의 Thevenin Theorem :Vg와 Vs차이점 (0) | 2023.06.01 |
| 전자장 Ch12.3.3 Gain Circle이란?(Simulation,Gonzalez, Pozar)*** (1) | 2023.05.27 |





