- 전자과 공대생 블로그(전자회로)
- 전자과 공대생 블로그2(전자기학)
- 배고픈 대학원생 (RF 아날로그)
- 나라발전 교수님 (아날로그)
- [VOD] IDEC 아날로그회로 - 고형호 교수님 (충…
- [VOD] IDEC 아날로그회로2
- [VOD] IDEC 아날로그회로3 - 이강윤 교수님(성…
- [VOD] IDEC 아날로그회로 직관적해석 - 심재윤 …
- [VOD] IDEC 아날로그 LNA - 고형호 교수님 …
- [VOD] Cadence OPAMP Verificati…
- [VOD] IDEC Full-Custom Flow 교육…
- [VOD] IDEC RF System-유형준 교수님(K…
- [VOD] IDEC 디지털 Cell-based 설계
- [VOD] IDEC PLL
- [VOD] IDEC CentOS 7 (Linux)
- [VOD] Band Gap Reference 정리
- [강의] 회로설계 멘토 삼코치
- [강의] OpAmp > CMFB
- [강의] 변박사님 : OpAmp, Radar
합법적사기꾼지망생
전자장 Ch02.2 Smith & Admittance Chart 본문
전자장 Ch02.2 Smith & Admittance Chart
평범한 민석이 2022. 12. 22. 16:24내용
1. Smith Chart
:Normalized Input Impedance 와 Input Reflection Coefficient는 1:1대응

위식의 양변을 Z0(특성저항)으로 나누면 Normalized Input Impedance에대한 공식이된다.

그리고 위식을통해서 Normalized Input Impedance 와 Input Reflection Coefficient는 1:1대응함을 알 수 있다.
이를 기반으로 Zin=r+jx와 Gamma_in(z=l)=실수부 + j 허수부를 연립해서 그래프를 그리면 Smith Chart가 된다.



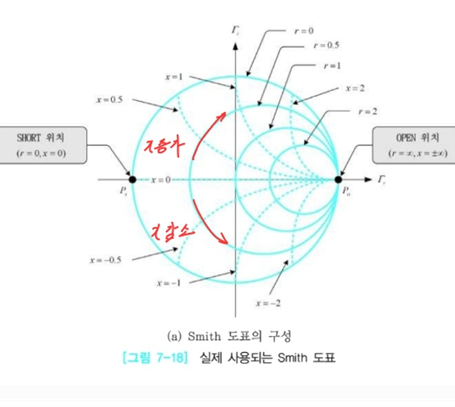
2. Admittance Chart
(1) Smith Chart를 180도 회전하면 Admittance Chart가 된다.
Z_LN을 알때 스미스차트상 해당지점에서 180도(λ/4)만큼 회전하면 Y_LN을 구할 수 있다. 이것은 Z_inN(l= λ/4 )을 이용해서 유도할 수 있다. 그리고 Z_inN(l)과 Y_inN(l)사이에도 이런관계가 존재하기때문에 Smith Chart와 Admittance Chart는 서로 180도 회전 관계에 놓인것이다.

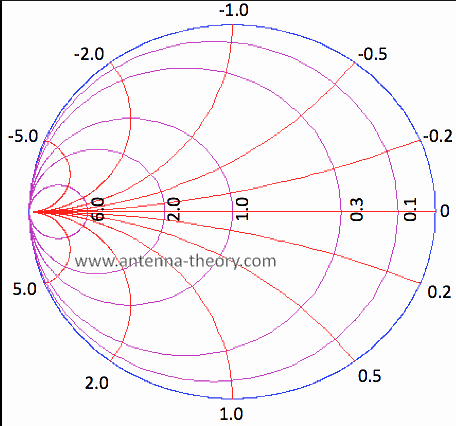
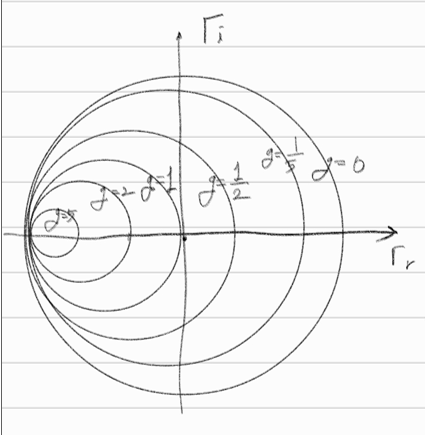
※ 주로 Smith&Admittance Chart를 사용한다.
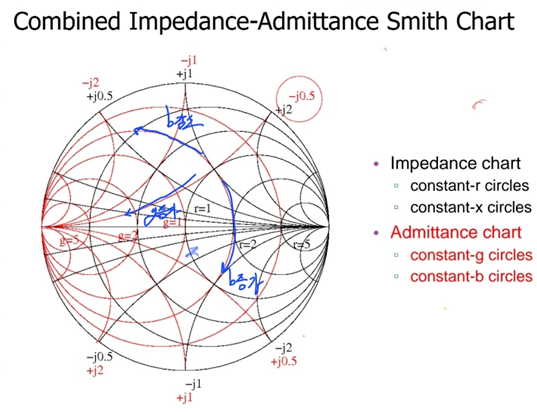
3. Smith & Admittance Chart 읽는법
(1) ZinN(z)을 기준으로 Gamma_in(z)를 읽는다.(Smith Chart)
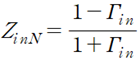
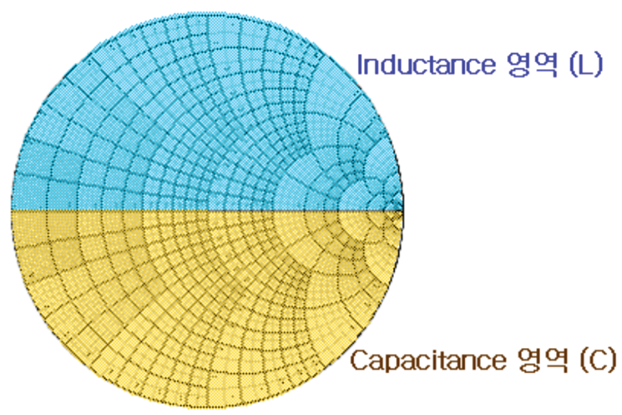
(2) YinN(z)을 기준으로 Gamma_in(z)를 읽는다.(Admittance Chart)
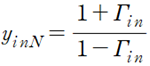
※ 주의사항 : Impedance와 Admittance는 역수관계이지만, Resistance(r)와 Conductance(g), Reactance(x)와 Susceptance(b)는 서로 역수관계가 아니다.
(3) 모든 Chart에서 위측은 Inductance(x>0, b<0)영역이고, 아래쪽은 Capacitance(x<0,b>0)영역이다.
(4) dmin과 dmax를 구하는 방법(전압이 최소 최대인 지점을 의미)
: arg〖{Γin} =-π〗 일 때의 전송선의길이(파장형태로 표현)를 읽으면 dmin이다.
arg〖{Γin} =π 〗 일 때 전송선의 길이를 읽으면 dmax이다.
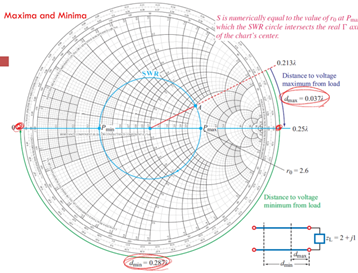
(5) 왼쪽 끝은 Short, 오른쪽 끝은 Open을 의미한다.
(6) 중앙은 무반사 상태(Matching)을 의미한다.
Special Cases
- Short : ZinN = 0 → Γin = -1
- Open : ZinN =∞ → Γin = 1
- Matching : ZinN = 1 → Γin = 0
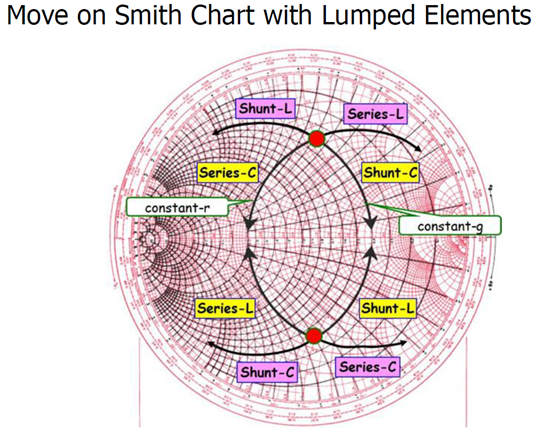
4. Smith & Admittance Chart상에서 Z_in(Gamma_in에 대응)이동 특성
(1) 직렬로 wire line혹은 electric element를 연결하면 Smith Chart를 따라 움직인다.(단, r, x 성분 중에서 하나가 고정인 등고선을 따라서 이동한다)
- 직렬 Resistance 추가 : Load에 추가 직렬 Resisitor를 추가하면 ZLN(=r+jx)의 r값이 증가한다. 그러면 x선을 따라서 우측으로 이동한다.
(r값이 커질수록 스미스차트상 우측으로 이동)(전력 손실 때문에 사용안함)
- 직렬 Reactance 추가 : Load에 추가 직렬 Inductor(=jwL)를 달면 ZLN(=r+jx)의 x값이 증가한다. 그러면 r선을 따라서 위로 이동한다.(x값이 커질수록 스미스차트상 위로 이동)
Load에 추가 직렬 Conductor(=1/jwC)를 달면 ZLN(=r+jx)의 x값이 감소한다. 그러면 r선을 따라서 아래로 이동한다.(x값이 커질수록 스미스차트상 위로 이동)
(2) 병렬로 wire line혹은 electric element를 연결하면 Admittance Chart를 따라 움직인다.(단, g, b 성분 중에서 하나가 고정인 등고선을 따라서 이동한다)
- 병렬 Susceptance 추가 : Load에 추가 병렬 Inductor(=1/jwL)를 달면 YLN(=g+jb)의 b값이 감소한다. 그러면 g선을 따라 위로 이동한다.(b값이 커질수록 스미스차트상 아래로 이동)
Load에 추가 병렬 Conductor(=jwC)를 달면 YLN(=g+jb)의 b값이 증가한다. 그러면 g선을 따라 아래로 이동한다.(b값이 커질수록 스미스차트상 아래로 이동)
- 병렬 Conductance 추가 : Load에 추가 병렬 Resistor(=Conductance)를 추가하면 YLN(=g+jb)의 g값이 증가한다. 그러면 b선을 따라서 좌측으로 이동한다.
(g값이 커질수록 스미스차트상 좌측으로 이동)(전력 손실 때문에 사용안함)
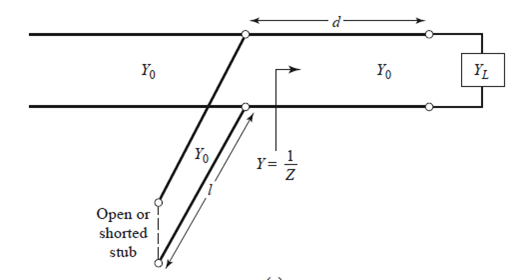
(3) 전송선 상 이동 :
Load에서 Generator방향으로 전송선을 따라 이동할때 시계방향(Wavelength Toward Generator)으로 움직인다. (한바퀴는 λ/2이다.)
*이때 |Γin|은 바뀌지 않는다. 이때 움직이는 원을 VSWR(Voltage Standing Wave Ratio) Circie이라고 한다.

(4) Freqence 증가 :
SmithChart상에서 달팽이 모양으로 감기면서 이동.
*그리고 이때 Matching 지점에 가장 가까운 지점에서의 Bandwidth가 넓을 수록 좋음을 나중에 RF에서 배울 것이다.
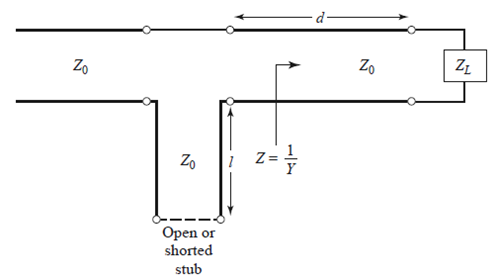
(5) 병렬 Open stub 추가 : Zin(OC) =-jZ_0 cotβl이고 ZinN(OC) = -j cotβl 이다.
그리고 YinN(OC) = j tanβl임을 알 수 있다.
병렬 Susceptance(Conductor)과 동일하게 g선을 따라 아래로 이동
(cotβl이 음수라면 g선을 따라 위로 이동)
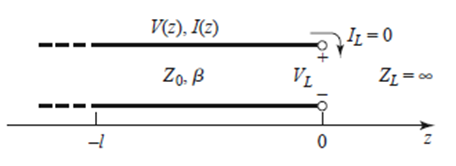
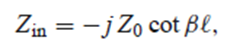
※ 증명과정
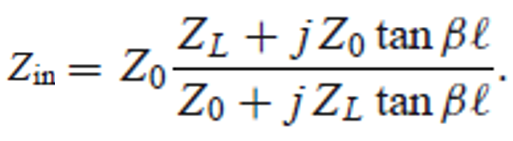
위 식에서 ZL을 무한대로 극한을 보내면된다.
(6) 병렬 Short stub 추가 : Zin(SC) = jZ_0 tanβl이고 ZinN(SC) = j tanβl 이다.
그리고 YinN(SC) = -j cotβl 임을 알 수 있다.
병렬 Susceptance(Inductor)과 동일하게 g선을 따라 위로 이동
(tanβl이 음수라면 g선을 따라 아래로 이동)
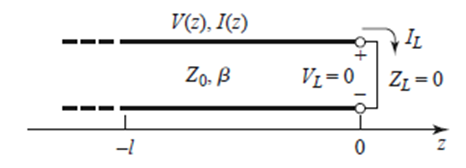
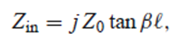
※ 증명과정
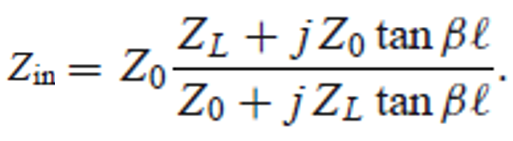
위 식에서 ZL을 0으로 극한을 보내면된다.
(7) 직렬 Open stub 추가 : Zin(OC) =-jZ_0 cotβl이고, ZinN(OC) =- j cotβl 이다.
직렬 Reactance(Capacitor)과 동일하게 r선을 따라 아래로 이동
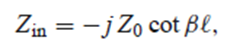
(8) 직렬 Short stub추가 : Zin(SC) =jZ_0 tanβl이고, ZinN(SC) =tanβl이다.
직렬 Reactance(Inductor)과 동일하게 r선을 따라 위로 이동
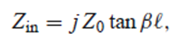
※ 총정리
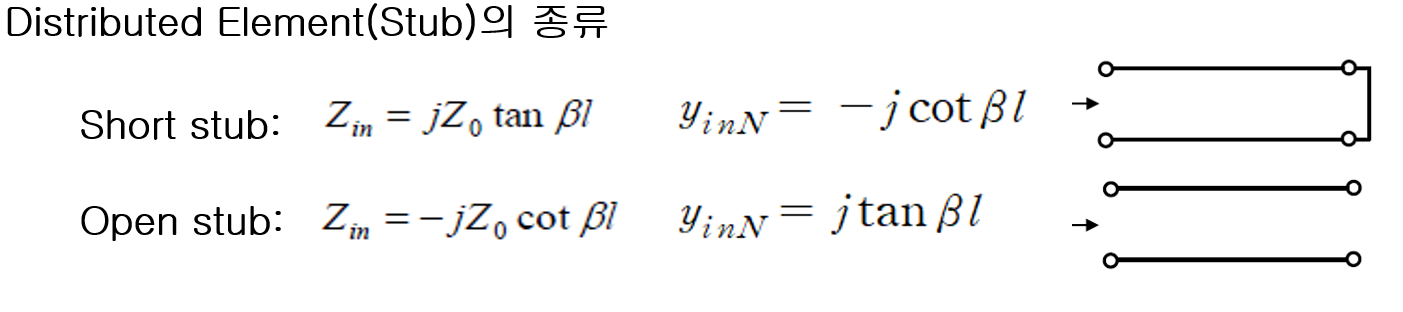
Distributed Elements으로 하는 매칭의 장단점 (Lumped Elements에 비해)
① Lumped L or C 소자가 필요없다.
② 쉽게 제작될수있다.(Easily fabricated)
③ 낮은 Q factor (넓은 대역폭) (참고 : Q 공진 회로에서 그 공진의 예리함을 나타내는 값)
④ 단점 : 저주파에서 회로의 사이즈가 커질 수 밖에 없다.
Reference
Pozar - Microwave Engineering
'A2_전자기학 & 전자장 > Microwave Engineering - Pozar' 카테고리의 다른 글
| 전자장 Ch01.2 맥스웰 방정식과 평면파(Uniform wave) (0) | 2023.01.16 |
|---|---|
| 전자장 Ch01.1 Microwave란? 분류(IEEE기준) (0) | 2023.01.16 |
| 전자장 Ch05.2 Matching with Distributed Elements (Single Stub Tunning) (0) | 2022.12.23 |
| 전자장 Ch05.1 Matching with Lumped Elements(L Network) (0) | 2022.12.22 |
| 전자장 Ch02.1 전송선 이론 (전자장 공식 총정리 포함) (3) | 2022.12.22 |




