- 전자과 공대생 블로그(전자회로)
- 전자과 공대생 블로그2(전자기학)
- 배고픈 대학원생 (RF 아날로그)
- 나라발전 교수님 (아날로그)
- [VOD] IDEC 아날로그회로 - 고형호 교수님 (충…
- [VOD] IDEC 아날로그회로2
- [VOD] IDEC 아날로그회로3 - 이강윤 교수님(성…
- [VOD] IDEC 아날로그회로 직관적해석 - 심재윤 …
- [VOD] IDEC 아날로그 LNA - 고형호 교수님 …
- [VOD] IDEC 아날로그집적회로 실습
- [VOD] Cadence OPAMP Verificati…
- [VOD] IDEC Full-Custom Flow 교육…
- [VOD] IDEC RF System-유형준 교수님(K…
- [VOD] IDEC 디지털 Cell-based 설계
- [VOD] IDEC PLL
- [VOD] IDEC CentOS 7 (Linux)
- [VOD] Band Gap Reference 정리
- [강의] 회로설계 멘토 삼코치
- [강의] OpAmp > CMFB
- [강의] 변박사님 : OpAmp, Radar
- [강의] PMIC - 박병하 교수님 (유료)
- [강의] 삼코치 -아날로그 회설 직무 (유료)
합법적사기꾼지망생
Ch2~3 회로그리기 이론적배경1 본문
우리에게 어떤 특정 조건을 만족시키는 회로지도 Map 을 만들라고 지시가 떨어졌을때 그회로를 만들어보자
만약 다음과 같은 조건을 만족 시키는 회로를 만들어야한다고 가정하자

이때 우선 우리는 1~3과정을 거친다.
1. truth table만든다.
truth table이란? input과 output 사이의 관계를 정리한 표이다.
tip)행은 (input의 갯수+output의 갯수)만큼 필요하고 열은 {2^(input의 갯수)}만큼 필요하다.
(다행히 이문제에서는 truth table이 이미주어져 있다.)
2. truth table을 minterm과 Maxterm의 방식으로 정리한다.
*minterm과 Maxterm이란?(feat.sum of product와 product of sum)(feat. only NAND gate와 only NOR gate)
minterm은 truth table에서 1의숫자가 가장 적도록하는것 sum of product(only NAND)를 나타낼때 쓴다.
Maxterm은 truth table에서 1의숫자가 가장 많도록 하는것 product of sum(only NOR)를 나타낼떄 쓴다.
그리고 minterm과 Maxterm은 서로 보수complement 관계에 놓여있다.

complement of m and M

minterm과 Maxterm을 표시해 보았다.
위 표에서 minterm과 maxterm의 예시를 들자면 다음과 같다.
m6= A'BC
M6 = m6'=(A'BC)' = A+B'+C'
그다음 단계로 가기위해 우리는 X에대한 Boolean algebra를 얻어야하고
그를위해서는 우선 minterm이나 Maxterm으로 표현해야한다
우선 minterm으로 표현하면 다음과 같다.

그림1
반대로 Maxterm으로 표현하면 다음과같다.

그림 2
3. Boolean algebra(simplifacation and optimization)으로 바꾼다.
그다음으로는 시그마(합을의 의미한다) 파이(곱을 의미한다)를 term들로 변환(ex. A'BC, ABC, A'B'C' 등등)하면 된다.
하지만 이외에 엄청편한 방법이 있다. 바로 truth table을 Gray Code(다음숫자사이에 1bit만 차이가 나는 숫자배열)을 이용한 K-map에 그리면된다.

Gray code 설명
이외에도 Boolean Cube라고 있는데 그것은 truth table을 그리는 다른 방법이다. 설명은
만약에 Sum of Product의 형태로 표현하라면 minterm을 이용하면된다. 그림 1의 내용을 Kmap에 정리하고 minterm의 관점으로 정리하면 다음과같이 Sum of Product의 boolean algebra가 나온다. 이 algebra (수식)는 가장 단순화되었고 그 회로에 최적화 되어있다. (이때 최적화란 delay와 Power(전력)을 최소화하기위해 gate수가 가장 적도록 회로를 설계하는 것을 의미한다.)

그림1의 Kmap(카르노맵)과 boolean algebra
그림 2의 내용을 Kmap에 정리하고 minterm의 관점으로 정리하면 다음과같이 Product of Sum의 boolean algebra가 나온다

그림2의 Kmap과 boolean algebra
*참고. 분배법칙 (A+B)' = A'*B' / (A*B)'=A'+B' (챕터2참고)
4.이제 회로를 그리면된다. minterm의 boolean algebra를 회로로 그리면 다음과 같다.
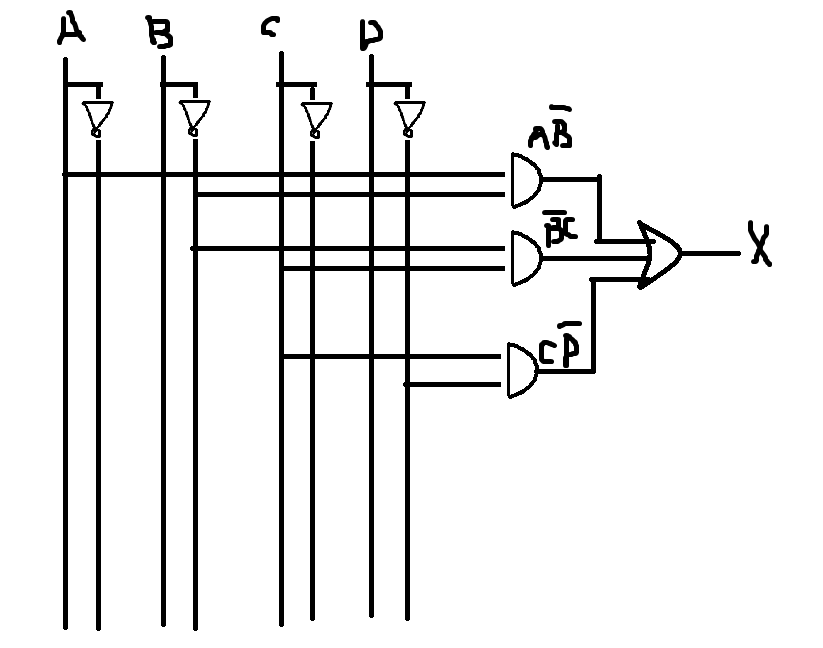
그림3
그런데 Ch2내용을 제대로 봤다면 알겠지만 ㅎㅎ 게이트는 AND, OR gate 보다 NAND, NOR gate가 더 작고 기본적인 모형이다. 그래서 우리는 이대로는 최적화가 됬다고 보기는 어렵다 그래서 쓰고자하는 이론이 (A')' =A 이다. 이것을 그림으로 표현하면 다음과 같다.

그리고 Ch2내용에 보면 알겠지만 다음 4가지 수식을 알고있어야한다.
inputs + Not gates + AND gate = NOR gate
inputs + AND gate+ Not gates = NAND gate
inputs + Not gates + OR gate = NAND gate
inputs + OR gate + Not gates = NOR gate
그러면 그림3에서 다음부분만을 NAND게이트로만 바꿀수 있다.

우선 Not게이트 각각에 도선에 2개씩 넣고

빨간색 부분을 input +AND+not 이니까 NAND로 바꿀 수 있다. 그러면 다음과 같이 된다.

그리고 그다음으로 나머지 빨간 부분도 inputs + Not gates + OR 이니까 NAND로 바꿀수 있다. 그러면 최종적으로 다음과 같이된다.

*참고로 Not 게이트도 NAND, NOR, XOR 게이트로 대체할 수 있다. 다음사진을 참조해라.
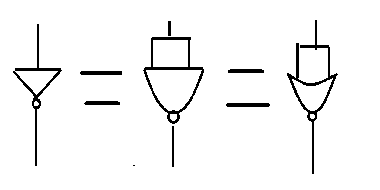
이제 방금 배운 것들을 적용해서 sum of product(minterm)을 다음그림과 같이 NAND 게이트로만 그릴 수있다.

마찬가지로 product of sum(Maxterm)을 NOR게이트로만 그릴수도있다.
이러한 원리로

다음과 같이 되는 것이다.

이렇게 Combinational Circuit을 만드는 것이다.
참고로 이외에도 Decoder(incoder)와 Multiplexer(MUX,deMUX)를 이용한 회로 설계도 있는데 그건 나중에 해보자 (참고로 미리말하자면 Decoder와 MUX만 있어도 모든 combinational circuit을 구현할 수있다.
'B1_디지털시스템 공학(velilog)' 카테고리의 다른 글
| Ch4-2 more combination circuit (arith metic units) (0) | 2019.10.08 |
|---|---|
| Ch4 combinational logic design_Decoder/ Multiplexer (0) | 2019.10.08 |
| Ch2 boolean algebra and logic gates (0) | 2019.10.08 |
| Ch1 binary numbers (0) | 2019.10.08 |
| 디지털 시스템 목차, Ch0 Digital & Analog (0) | 2019.10.08 |




