합법적사기꾼지망생
9.1.1 대신호 Parameters( Y, Z, Γ, G, LSSP ≒ X-parameter ) 본문
9.1.1 대신호 Parameters( Y, Z, Γ, G, LSSP ≒ X-parameter )
평범한 민석이 2023. 11. 17. 16:290. Large-signal의 가장 큰 특징
(1) Harmonic 성분이 존재한다. (Taylor Series)
(2) Non-linear하다 → Input신호의 크기에 따라, Gain(혹은 Y, Z, Γ 등)의 Magnitude와 Phase가 달라진다.
(3) Harmonic Balance(큰신호의 변화, Piecewise Linear Modeling), Period Steady State Simulation으로 측정함
(4) 대신호는 소신화 다르게 I, V, Z, Y, Γ 사이의 1:1 변환이 불가능하다.
1. Large-signal Admittance
Nonlinear 소자의 양단에 걸리는 전류는 아래와 같이 나타난다.자세한것은 아래의 링크 참조*
이때, Nonlinear 소자의특성에 의해서 I_1과 φ_1은 V에대한 함수가 된다.
그러면 Fundamental 신호에 대한 Admittance는 아래와 같이 정의된다.
2. Large-signal Impedance
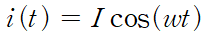
임피던스도 1번의 어드미턴스와 비슷한 원리로 정의된다.
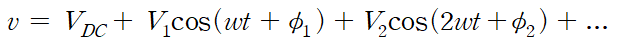
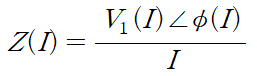
3. Large-signal Reflection Coefficient(Large-Signal S-Parameter도 비슷한 원리)
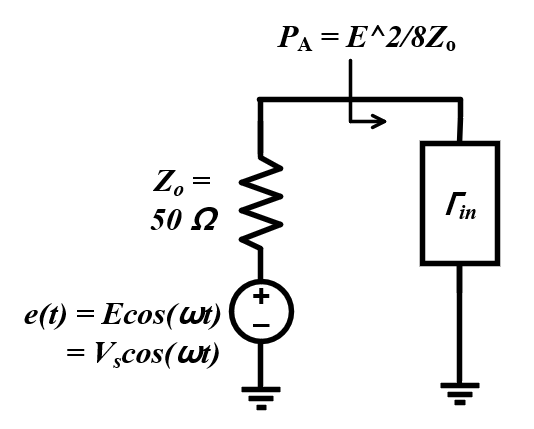
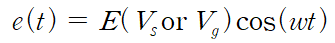
우선 위처럼 입력포트 (50)옴을통해서 전력신호를 보낸다고 하자, 이때 진폭을 E혹은 V_source라고 정의하자
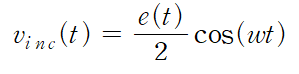
이때, Γin으로 들어갈 수 있는 최대 전압은 전압분배 법칙에 의해서 위와 같을 것이다.
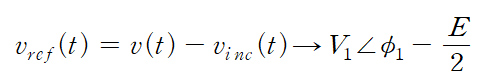
그리고 이를 기반으로 Total Voltage에서 입사되는 신호를 빼주면 reflected 신호를 구할 수 있다. (화살표 이후로 Phasor로 변환하였다. Γ또한 Phasor 형태로 표현하기 위해서이다.)
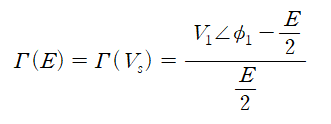
그러면 대신호 반사계수(Large-signal Reflection Coefficient)는 위와 같이 정의할 수 있다. 이때 주의할 점이 V_1, φ또한 E(입련전압진폭)에 대한 함수라는 점이다.
※ Large-signal S-parameter(LSSP) ≒? X-parameter = the parameters of the Poly-Harmonic Distortion (PHD) nonlinear behavioral model.
X-parameters are a generalization of S-parameters and are used for characterizing the amplitudes and relative phase of harmonics generated by nonlinear components under large input power levels.
X-parameters - Wikipedia
From Wikipedia, the free encyclopedia Agilent engineer demonstrates X-parameter functionality at IEEE MTT-S International Microwave Symposium, Boston MA June 10, 2009.) X-parameters are a generalization of S-parameters and are used for characterizing the a
en.wikipedia.org
4. Large-signal Gain
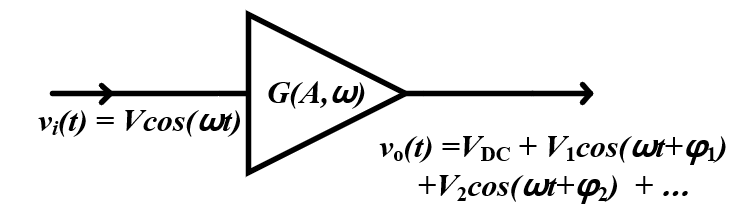
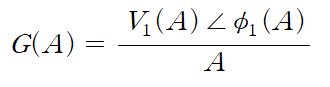
Voltage Amp의 Large-signal VoltageGain또한 위처럼 A(input Amplitude)에대한 함수형태로 표현된다.(원인, Nonlinearity) 이는 Harmonic Balance을통해 Conversion Gain으로 표현되기도 한다.
*참조
2.2 Effects of Nonlinearity (tistory.com)
2.2 Effects of Nonlinearity
내용 1. Harmonic Distortion : Fundamental 성분이 Harmonic성분에의해서 변하는 것을 의미한다. (1) Non-linear, Memoryless, Time-Invariant System의 근사화 위 식을 근사화 해보자. 아래와 같이 될것이다.(2.25 식) 위 식
tgs05016.tistory.com
RF공학 Ch02. Nonlinearity > Harmonic (4th harmonic 고려) (tistory.com)
RF공학 Ch02. Nonlinearity > Harmonic (4th harmonic 고려)
이에 4차 성분까지 포함시키기위해 (cos wt)^4 를 계산하면 다음과 같습니다. (cos^2(θ) = (1 + cos(2θ)) / 2를 공식을 적용하면 아래와 같이 변합니다.) (cos wt)^4 = [cos^2(wt)]^2 = [(1 + cos(2wt)) / 2]^2 (cos wt)^4 = (1
tgs05016.tistory.com
'A2-4_능동초고주파 회로설계입문 > Oscillator' 카테고리의 다른 글
| 9.1.3 직렬 병렬 발진의 Duality(+CCNR, VCNR 이란?) (3) | 2023.11.17 |
|---|---|
| *9.1.2 발진(Oscillation)의 종류 및 판별 : One-port point of view의 확장(Razavi, Pozar) ... 소신호 & 대신호 관점 (0) | 2023.11.17 |
| 9.0.2 직렬 병렬 RLC회로의 완전응답 (sinsoidal total response)(feat. 전기회로1,2) (0) | 2023.11.17 |
| 9.0.1 발진기에 대한 이론적 배경( 기존 해석방법들 ) (1) | 2023.11.15 |
| 9.0.3.α 발진은 한 주파수에 대해서만 일어나는 것이 아니다! (0) | 2023.10.08 |
