합법적사기꾼지망생
9.0.1 발진기에 대한 이론적 배경( 기존 해석방법들 ) 본문
0. 이론적배경
(1) Input Port의 방향 : 직렬 및 병렬 판별법*
- 그냥 단순히 해당 해당 지점에 Port를 달고 Loop를 끊으면된다.
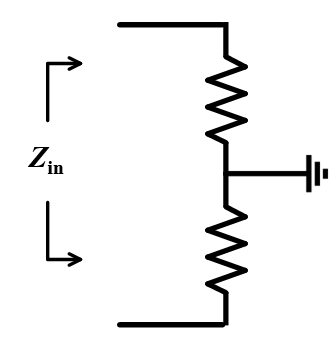
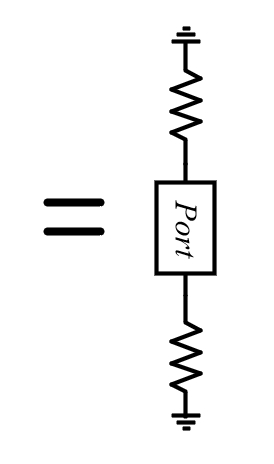
예를들어 위의 Zin은 Port 상하로 Resistor가 "Series"로 달려 있음을 쉽게 파악할 수 있다. 즉 Zin = 2R이다.
그래서 RF Differential Circuit을 설계할때 50Ohm이 아닌 100Ohm Port를 사용하는 것이다.
1. Large-signal vs. Small-signal (단, Oscillator 관점)
(1) Oscillator의 states
- transient : start-up, grow-up, damping(underdamping, overdamping, critical damping)
- steady-state
(2) Large-signal vs. Small-signal
Large-signal System = Non-linear Time-Varying System = steady-state, grow-up, damping of Oscillator
Small-signal System = Linear Time-Invariant System = start-up of Oscillator
(3) Passive Devices vs. Active Devices
- Passive Device : Large-signal과 Small-signal이 같다.(∵ L-TI System)
- Active Device : Large-signal과 Small-signal이 다르다.(∵ non Linear-TV System)
2. B. Razavi의 발진기 해석
(1) Feedback View of Oscillator : Loop Gain
- Barkhuassen Oscillation Criterion, Nyquist Stability Criterion, Bode Stability Criterion ... 참조*
- 저주파에서 자주 사용하는 기법(이유 : Loop의 갯수가 적고, 선로 사이에 Coupling이 약하기 때문이다.)*
※ 장점 : Oscillation에대한 가장 쉬운 이해, Phase Noise, Pout에대한 상대적으로 쉬운 분석
※ 한계 : Feedback 자체가 현실에 완벽하게 적용되지 않는 이론(Loop Gain을 구할려면 Loop 중간을 잘라야하는데 여기서 정확도가 떨어진다), 현실에 가깝게 풀려면 Small-signal model + Kirchhoff 법칙으로 풀어야한다. 36_Bode-Network Analysis And Feedback Amplifier Design(1975) 책을 보면 좀 더 현실에 가까운 Feedback에 대한 분석 이 나와있다.
(2) One-Port View of Oscillator 해석 : Negative Resistance
- Negative Resistance에 대한 사전 이해가 필요하다. ... 참조*
- 고주파에서 자주 사용하는 기법 (이유 : Loop의 갯수가 많고, 선로 사이에 Coupling이 강하기 때문이다.)*
- Positive Resistance라고 해서 Network 내부의 발진을 모두 잡지 못한다.* 즉, Positive Resistance로 Stability를 판별하려면 모든 내부 Node들에 대해서 Positive Resistance를 확인해야한다.
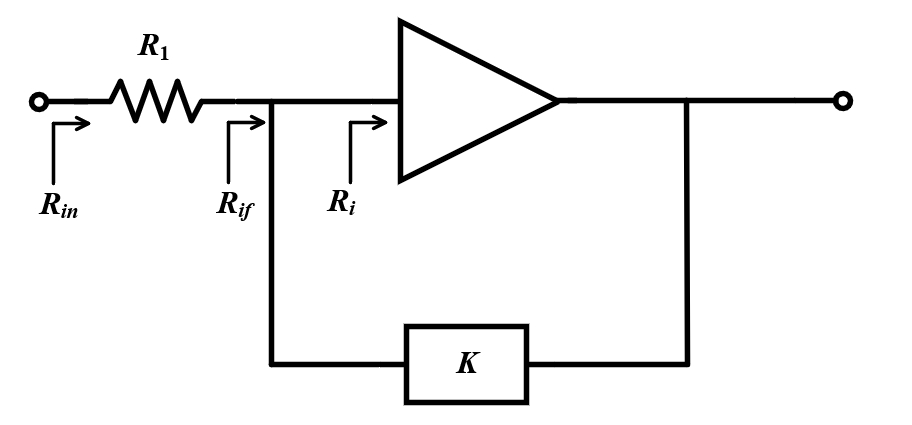
(3) Negative Resistance 해석과 Positive Feedback 해석의 연결점
- 사실 Negative Resistance 해석과 Positive Feedback은 동일한 현상에대한 다른 해석일 뿐이다.*
(4) 구체적인 원리는 참조 4번*
3. D. Pozar의 발진기 해석
(1)Pozar 또한 Razavi와 마찬가지로 One-Port View of Oscillator를 Microwave 관점에서 설명하였다.
(2) 요약 : 반사계수가 1보다 큼 = Negative Resistance = Negative Admittance, 입력에서 발진 ↔ 출력에서 발진, Kurokawa Oscillation Criterion, Stability Circle
(3)주의사항, Negative Resistance라고 발진하는 것은 아니다. Unstable(발진가능성)한 것이다. Load에 무엇이 달리는냐에 따라서 발진할 수도 혹은 발진 안할 수도 있다.
주의사항 정리
Oscillation → Negative Impedance (O) (but .. only at Oscillation Start-up Point)
Oscillation ← Negative Impedance (X) (∵ Unstable ≠ Oscillation)
Stable System → Positive Impedance (O) (∵ Pozar, Loop Gain ΓLΓin can be < 1)
Stable System ← Positive Impedance (X) (∵ Negative Resistance + Large series Resistor = Positive Resistance but it can oscillate)
(4) 구체적인 원리는 참조 3번*
4. Gonzalez, 염경환의 발진기해석
(1) Pozar의 해석의 좀 더 일반적인 해석을 Gonzalez - Foundations of Oscillator Circuit (2007)에서 볼 수 있고,
곤잘레스와 조금 다른 관점을 염경환 - 능동초고주파 회로설계입문 에서 볼 수 있다.
5. Inder J. Bahl, 발진의 분류
Even Mode 발진 vs. Odd Mode 발진
Fundamentals of RF and Microwave Transistor Amplifiers - (Inder J. Bahl)
출처
참조*
0. DM의 Zc가 100옴인 이유
Differential Port의 특성저항(Characteristic Impedance)이 100 Ohm인 이유 (tistory.com)
Differential Port의 특성저항(Characteristic Impedance)이 100 Ohm인 이유
결론: 결론부터 이야기하자면, Input Impedance들이 모두 2배가 되므로 Normalize 해야하는 값도 2배가 되어야 50 Ohm Port로 Normalized된 Smith Chart상에서 동일하게 해석이 가능하다. 원리 : Differential System의 I
tgs05016.tistory.com
1. Negative Resistance = Positive Feedback
전자장 Ch13.1.2 Stability/Oscillation Criteria 총정리(전자회로,제어공학,전자장) (tistory.com)
전자장 Ch13.1.2 Stability/Oscillation Criteria 총정리(전자회로,제어공학,전자장)
발진을 확인하는 가장 확실한 방법 : 회로의 출력 Node에 Port 달지 말고(혹은 특성저항이 infinite인 Port를 달고) Labeling만 해서, Time-Transient를 돌려서 FFT했을때, 발진하는 지 알 수 있다.(※ 만약 발진
tgs05016.tistory.com
2. 전자기학 발진기 > Barhaussen Oscillation Criterion
전자회로2_12 : Oscilator 발진기 정리 PDF (tistory.com)
전자회로2_12 : Oscilator 발진기 정리 PDF
내용
tgs05016.tistory.com
3. RFDH 내용정 > 발진의 원인 Loop > 고주파에선 Loop Gain으로 발진을 보기 어려운 이유 , Negative Resistance = Positive Feedback(특히, oscillation 상황)
전자장 Ch12.2+α. Negative Resistance Analysis (tistory.com)
전자장 Ch12.2+α. Negative Resistance Analysis
이론적 배경 Negative Impedance이면 Unstable이다. Oscillation이 아니다. (물론 Positive Impedance라고해서 Stable 한 것도 아니다. 반례 : Oscillator + Resistor + port(TermG) 달아서 Zin 보면 positive impedance임에도 발진함
tgs05016.tistory.com
4. Pozar의 Microwave Oscillator One-port 해석
전자장 Ch13.2 Microwave Oscillator (+ Kurokawa's condition) (tistory.com)
전자장 Ch13.2 Microwave Oscillator (+ Kurokawa's condition)
기존 발진의 정의 : Bakhausen Criterion, Positive Feedback, K-factor 등등과 비교하면서 생각해보자 (제어공학,전기회로, 전자회로) 사전 내용 RF 회로개념 잡기 - PART 2 ▶ Oscillator (발진기) (rfdh.com) RF 회로개
tgs05016.tistory.com
5. Razavi의 One-port Negative Resistance Oscillator 분석
8.2.2 One-Port View of Oscillator (LC tank 병렬 발진) (tistory.com)
8.2.2 One-Port View of Oscillator (LC tank 병렬 발진)
1. 발진기 분류 (1) Req > 0, transient.damping or Stable System ... small-signal or large-signal (2) Req = 0, steady-state.LC resonance (feat. LC tank) ... large-signal (224) LC Oscillator Tank Circuit - YouTube (3) Req < 0, transient.start-up or grow-
tgs05016.tistory.com
6. Inder J. Bahl
: https://tgs05016.tistory.com/entry/RF전공자-필수교재RF-회로설계-Radar-이미징-안테나-PA-Matching-등 [합법적사기꾼지망생:티스토리]
'A2-4_능동초고주파 회로설계입문 > Oscillator' 카테고리의 다른 글
| 9.1.3 직렬 병렬 발진의 Duality(+CCNR, VCNR 이란?) (3) | 2023.11.17 |
|---|---|
| *9.1.2 발진(Oscillation)의 종류 및 판별 : One-port point of view의 확장(Razavi, Pozar) ... 소신호 & 대신호 관점 (0) | 2023.11.17 |
| 9.0.2 직렬 병렬 RLC회로의 완전응답 (sinsoidal total response)(feat. 전기회로1,2) (0) | 2023.11.17 |
| 9.1.1 대신호 Parameters( Y, Z, Γ, G, LSSP ≒ X-parameter ) (0) | 2023.11.17 |
| 9.0.3.α 발진은 한 주파수에 대해서만 일어나는 것이 아니다! (0) | 2023.10.08 |
